题目内容
若函数y=x3-3bx+3b在(0,1)内有极小值,则
| A.0<b<1 | B.b<1 |
| C.b>0 | D.b<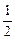 |
A
本题主要考查应用导数解决有关极值与参数的范围问题.
极值点是导数为零的点.∵函数在(0,1)内有极小值,∴极值点在(0,1)上.令y′=" " 3x2-3b=0,得x2=b,显然b>0,
∴x=± .又∵x∈(0,1).∴0<
.又∵x∈(0,1).∴0< <1.∴0<b<1.
<1.∴0<b<1.
极值点是导数为零的点.∵函数在(0,1)内有极小值,∴极值点在(0,1)上.令y′=" " 3x2-3b=0,得x2=b,显然b>0,
∴x=±
 .又∵x∈(0,1).∴0<
.又∵x∈(0,1).∴0< <1.∴0<b<1.
<1.∴0<b<1.
练习册系列答案
相关题目
 上任意一点,则点P到直线
上任意一点,则点P到直线 的最小距离是 ( )
的最小距离是 ( )



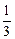 ,则
,则 在区间
在区间 上的最大值是
上的最大值是
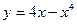 ,在
,在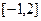 上的最大、最小值分别为( )
上的最大、最小值分别为( )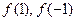
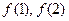
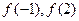
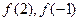
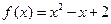 的极值是( )
的极值是( )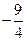
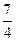
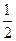
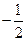
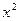 -
-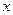 ,则
,则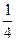 C
C 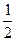 D
D