题目内容
已知函数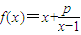 (p为常数且p>0),若f(x)在区间(1,+∞)的最小值为4,则实数p的值为 .
(p为常数且p>0),若f(x)在区间(1,+∞)的最小值为4,则实数p的值为 .
【答案】分析:将函数f(x)配成基本不等式的形式,然后利用基本不等式的性质进行求解.
解答:解:∵函数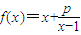 =x-1+
=x-1+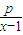 +1≥2
+1≥2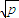 +1(当且仅当x-1=
+1(当且仅当x-1=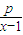 等号成立),
等号成立),
∴2 +1=4,
+1=4,
∴p= ,
,
∴(x-1)=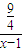 ,
,
解得x= 或-
或- ,
,
∴实数p= ,
,
故答案为 .
.
点评:此题考查基本不等式的性质及其应用,是一道基础题.
解答:解:∵函数
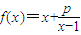 =x-1+
=x-1+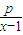 +1≥2
+1≥2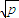 +1(当且仅当x-1=
+1(当且仅当x-1=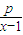 等号成立),
等号成立),∴2
 +1=4,
+1=4,∴p=
 ,
,∴(x-1)=
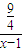 ,
,解得x=
 或-
或- ,
,∴实数p=
 ,
,故答案为
 .
.点评:此题考查基本不等式的性质及其应用,是一道基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
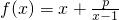 (p为常数且p>0),若f(x)在区间(1,+∞)的最小值为4,则实数p的值为
(p为常数且p>0),若f(x)在区间(1,+∞)的最小值为4,则实数p的值为 ; (2)
; (2)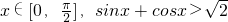 ;(3)正项等比数列{an}中:a4.a6=8,函数f(x)=x(x+a3)(x+a5)(x+a7),则
;(3)正项等比数列{an}中:a4.a6=8,函数f(x)=x(x+a3)(x+a5)(x+a7),则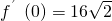 ;(4)若数列{an}的前n项和为Sn=2n2-n+1,且bn=2an+1,则数列{bn}前n项和为Tn=4n2-n+2上述命题正确的序号是________.
;(4)若数列{an}的前n项和为Sn=2n2-n+1,且bn=2an+1,则数列{bn}前n项和为Tn=4n2-n+2上述命题正确的序号是________. (p为常数且p>0),若f(x)在区间(1,+∞)的最小值为4,则实数p的值为
(p为常数且p>0),若f(x)在区间(1,+∞)的最小值为4,则实数p的值为 ; (2)
; (2) ;(3)正项等比数列{an}中:a4.a6=8,函数f(x)=x(x+a3)(x+a5)(x+a7),则
;(3)正项等比数列{an}中:a4.a6=8,函数f(x)=x(x+a3)(x+a5)(x+a7),则 ;(4)若数列{an}的前n项和为Sn=2n2-n+1,且bn=2an+1,则数列{bn}前n项和为Tn=4n2-n+2上述命题正确的序号是 .
;(4)若数列{an}的前n项和为Sn=2n2-n+1,且bn=2an+1,则数列{bn}前n项和为Tn=4n2-n+2上述命题正确的序号是 .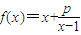 (p为常数且p>0),若f(x)在区间(1,+∞)的最小值为4,则实数p的值为 .
(p为常数且p>0),若f(x)在区间(1,+∞)的最小值为4,则实数p的值为 .