题目内容
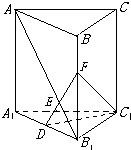 20、如图,直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1中,已知AC=BC=AA1=a,∠ACB=90°,F是棱BB1上的中点,D 是A1B1中点,求证:A1B∥面C1DF.
20、如图,直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1中,已知AC=BC=AA1=a,∠ACB=90°,F是棱BB1上的中点,D 是A1B1中点,求证:A1B∥面C1DF.分析:欲证A1B∥面C1DF,根据直线与平面平行的判定定理可知只需证A1B与面C1DF内一直线平行即可,根据中位线定理可知A1B∥DF,DF?面C1DF,A1B?面C1DF,满足定理所需条件.
解答:证明:∵F是棱BB1上的中点,D 是A1B1中点,
∴A1B∥DF
∵DF?面C1DF,A1B?面C1DF
∴A1B∥面C1DF.
∴A1B∥DF
∵DF?面C1DF,A1B?面C1DF
∴A1B∥面C1DF.
点评:本题主要考查了直线与平面平行的判定,应熟练记忆直线与平面平行的判定定理,属于基础题.

练习册系列答案
相关题目
如图,直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其左视图的面积为( )


| A、4 | ||
B、
| ||
C、2
| ||
| D、2 |
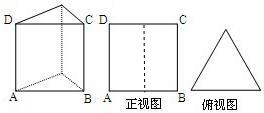 如图,直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其左视图的面积为
如图,直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其左视图的面积为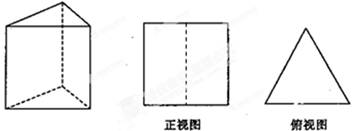
 B.
B.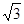 C.4
D.2
C.4
D.2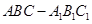 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中, 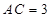 ,
,
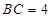 ,
,
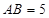 ,
,
 ,点
,点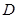 是
是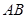 的中点.
的中点. 
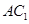 ∥平面
∥平面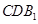 ;
;