题目内容
已知向量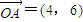 ,
,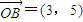 ,且
,且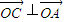 ,
,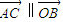 ,则向量
,则向量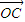 = .
= .
【答案】分析:设出向量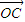 的坐标,根据两个向量的减法运算得到向量
的坐标,根据两个向量的减法运算得到向量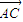 的坐标,再根据两个向量的平行和垂直关系得到两组向量的坐标之间的关系,平行和垂直放在一起用,不要把两种关系的充要条件弄混,特别是中间的符号,再解方程组即可.
的坐标,再根据两个向量的平行和垂直关系得到两组向量的坐标之间的关系,平行和垂直放在一起用,不要把两种关系的充要条件弄混,特别是中间的符号,再解方程组即可.
解答:解:设向量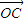 =(x,y)
=(x,y)
∵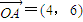 ,
,
∴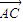 =
=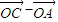 =(x-4,y-6),
=(x-4,y-6),
∵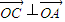 ,
,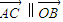 ,
,
∴4x+6y=0,①
5(x-4)-3(y-6)=0,②
∴x= ,y=-
,y=-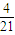
∴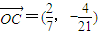
故答案为:(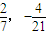 )
)
点评:本题是一个向量之间关系的平行和垂直关系的问题,是把向量的几何关系转化为代数运算的问题,特别注意连接代数式之间的符号,注意平行和垂直充要条件不要用错.
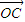 的坐标,根据两个向量的减法运算得到向量
的坐标,根据两个向量的减法运算得到向量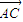 的坐标,再根据两个向量的平行和垂直关系得到两组向量的坐标之间的关系,平行和垂直放在一起用,不要把两种关系的充要条件弄混,特别是中间的符号,再解方程组即可.
的坐标,再根据两个向量的平行和垂直关系得到两组向量的坐标之间的关系,平行和垂直放在一起用,不要把两种关系的充要条件弄混,特别是中间的符号,再解方程组即可.解答:解:设向量
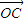 =(x,y)
=(x,y)∵
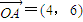 ,
,∴
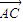 =
=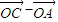 =(x-4,y-6),
=(x-4,y-6),∵
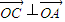 ,
,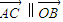 ,
,∴4x+6y=0,①
5(x-4)-3(y-6)=0,②
∴x=
 ,y=-
,y=-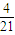
∴
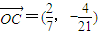
故答案为:(
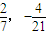 )
)点评:本题是一个向量之间关系的平行和垂直关系的问题,是把向量的几何关系转化为代数运算的问题,特别注意连接代数式之间的符号,注意平行和垂直充要条件不要用错.

练习册系列答案
相关题目
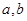 满足
满足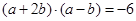 ,且
,且 ,
,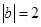 ,则a与b的夹角为
.
,则a与b的夹角为
.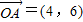 ,
, ,且
,且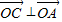 ,
,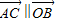 ,则向量
,则向量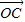 = .
= . 满足
满足 ,且
,且 ,
, ,则
,则 等于( )
等于( )

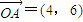 ,
, ,且
,且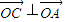 ,
,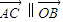 ,则向量
,则向量 = .
= .