题目内容
过抛物线y2=4x顶点O的直线l1、l2与抛物线的另一个交点分别为A、B,l1⊥l2,OD⊥AB,垂足为D,则D点的轨迹方程为( )
| A、y2=x(x≠0) | ||
B、
| ||
| C、(x-2)2+y2=4(x≠0) | ||
| D、(x-2)2+y2=4 |
分析:设出直线OA的方程,根据l1⊥l2,可得直线OB的方程,联立方程组,分别求出点A和点B,得到直线AB的方程,发现直线AB恒过定点(4,0),利用几何关系可得点D到定点(2,0)的距离等于定长2,可得点D的轨迹方程.
解答: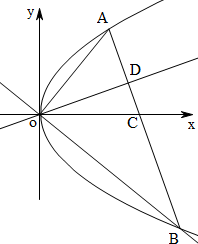 解:设直线OA的方程为y=kx,则
解:设直线OA的方程为y=kx,则
,消去y得x=
,
∴点A的坐标为(
,
),
∵l1⊥l2,
∴直线OA的方程为y=-
x,点B的坐标为(4k2,-4k),
则直线AB的斜率为
=
,
∴直线AB的方程为y+4k=
(x-4k2),
整理可得,y=
(x-4),
故直线AB经过定点(4,0),
∵OD⊥AB,垂足为D,则OD的垂直平分线必定经过点(2,0),
∴点(2,0)到原点O的距离等于到点D的距离,
又点(2,0)到原点O的距离为2,
∴点D到定点(2,0)的距离恒为定值2,
根据圆的定义可知,点D的轨迹是一个以(2,0)为圆心,2为半径的一个圆,
∴点D的轨迹方程为(x-2)2+y2=4,
故选:D.
 解:设直线OA的方程为y=kx,则
解:设直线OA的方程为y=kx,则
|
| 4 |
| k2 |
∴点A的坐标为(
| 4 |
| k2 |
| 4 |
| k |
∵l1⊥l2,
∴直线OA的方程为y=-
| 1 |
| k |
则直线AB的斜率为
| ||
|
| k |
| 1-k2 |
∴直线AB的方程为y+4k=
| k |
| 1-k2 |
整理可得,y=
| k |
| 1-k2 |
故直线AB经过定点(4,0),
∵OD⊥AB,垂足为D,则OD的垂直平分线必定经过点(2,0),
∴点(2,0)到原点O的距离等于到点D的距离,
又点(2,0)到原点O的距离为2,
∴点D到定点(2,0)的距离恒为定值2,
根据圆的定义可知,点D的轨迹是一个以(2,0)为圆心,2为半径的一个圆,
∴点D的轨迹方程为(x-2)2+y2=4,
故选:D.
点评:本题主要考查了交点轨迹问题,此题为教材习题的改编题,其中直线AB经过定点(4,0)是解题的关键,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 =0,求以OA、OB为直径的两圆的另一个交点P的轨迹.
=0,求以OA、OB为直径的两圆的另一个交点P的轨迹.