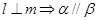题目内容
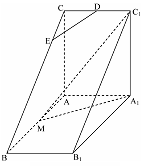
如图,直三棱柱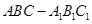 中,
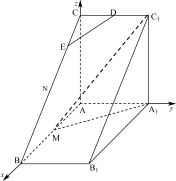
中,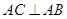 ,
,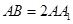 ,
,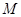 是
是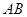 的中点,△
的中点,△ 是等腰三角形,
是等腰三角形,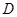 为
为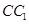 的中点,
的中点,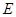 为
为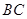 上一点.
上一点.
(1)若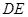 ∥平面
∥平面 ,求
,求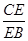 ;
;
(2)求直线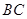 和平面
和平面 所成角的余弦值.
所成角的余弦值.
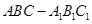 中,
中,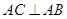 ,
,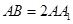 ,
,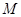 是
是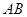 的中点,△
的中点,△ 是等腰三角形,
是等腰三角形,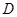 为
为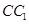 的中点,
的中点,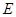 为
为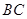 上一点.
上一点.
(1)若
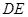 ∥平面
∥平面 ,求
,求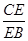 ;
;(2)求直线
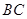 和平面
和平面 所成角的余弦值.
所成角的余弦值.(1)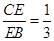 ;(2)
;(2)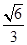 .
.
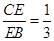 ;(2)
;(2)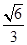 .
.试题分析:本题主要考查线线平行、线面平行、线线垂直、线面垂直、线面角、向量法等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,取BC中点,由中位线及平行线间的传递性,得到
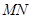 ∥
∥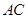 ∥
∥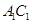 ,即
,即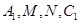 四点共面,利用线面平行的性质,得
四点共面,利用线面平行的性质,得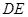 ∥
∥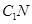 ,从而得到E是CN中点,从而得到
,从而得到E是CN中点,从而得到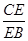 的值;第二问,连结
的值;第二问,连结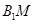 ,利用直三棱柱,得
,利用直三棱柱,得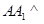 平面
平面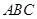 ,利用线面垂直的性质得
,利用线面垂直的性质得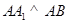 ,从而得到
,从而得到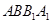 为矩形且
为矩形且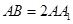 ,所以
,所以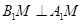 ,利用线面垂直得到线线垂直
,利用线面垂直得到线线垂直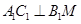 ,2个线线垂直得到线面垂直,由于
,2个线线垂直得到线面垂直,由于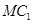 是
是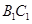 摄影,所以
摄影,所以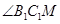 为线面角,在
为线面角,在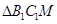 中解出
中解出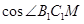 的值.
的值.试题解析:『法一』(1)取
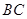 中点为
中点为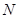 ,连结
,连结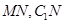 , 1分
, 1分∵
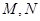 分别为
分别为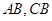 中点
中点∴
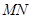 ∥
∥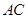 ∥
∥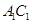 ,
,∴
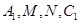 四点共面, 3分
四点共面, 3分且平面
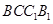
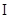 平面
平面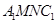
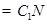
又
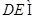 平面
平面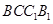 ,
,且
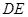 ∥平面
∥平面
∴
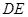 ∥
∥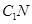
∵
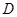 为
为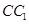 的中点,∴
的中点,∴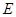 是
是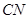 的中点, 5分
的中点, 5分∴
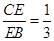 . 6分
. 6分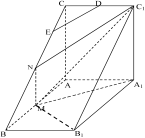

(2)连结
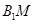 , 7分
, 7分因为三棱柱
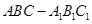 为直三棱柱,∴
为直三棱柱,∴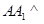 平面
平面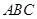
∴
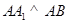 ,即四边形
,即四边形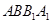 为矩形,且
为矩形,且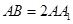
∵
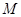 是
是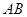 的中点,∴
的中点,∴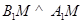 ,
,又
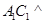 平面
平面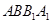 ,
,∴
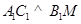 ,从而
,从而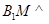 平面
平面 9分
9分∴
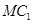 是
是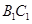 在平面
在平面 内的射影
内的射影∴
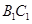 与平面
与平面 所成的角为∠
所成的角为∠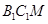
又
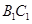 ∥
∥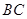 ,
,∴直线
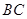 和平面
和平面 所成的角即
所成的角即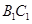 与平面
与平面 所成的角10分
所成的角10分设
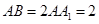 ,且三角形
,且三角形 是等腰三角形
是等腰三角形∴
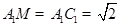 ,则
,则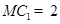 ,
,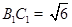
∴

∴直线
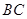 和平面
和平面 所成的角的余弦值为
所成的角的余弦值为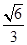 . 12分
. 12分『法二』(1)因为三棱柱
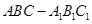 为直三棱柱,
为直三棱柱,∴
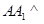 平面
平面 ,又
,又
∴以
 为坐标原点,分别以
为坐标原点,分别以
所在直线为
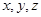 轴,
轴,建立如图空间直角坐标系. 1分

设
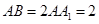 ,又三角形
,又三角形 是
是等腰三角形,所以
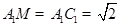
易得
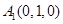 ,
,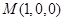 ,
,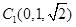 ,
,所以有
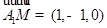 ,
,
设平面
 的一个法向量为
的一个法向量为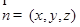 ,则有
,则有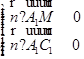 ,即
,即 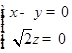 ,令
,令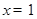 ,有
,有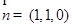 4分
4分(也可直接证明
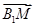 为平面
为平面 法向量)
法向量)设
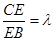 ,
,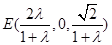 ,又
,又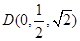 ,
,∴
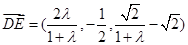
若
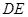 ∥平面
∥平面 ,则
,则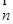
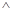
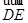 ,所以有
,所以有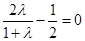 ,
,解得
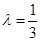 ,∴
,∴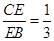 6分
6分(2)由(1)可知平面
 的一个法向量是
的一个法向量是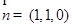 ,
,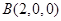 ,
,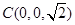 ,求得
,求得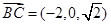
设直线
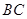 和平面
和平面 所成的角为
所成的角为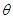 ,
,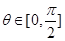 ,
,则
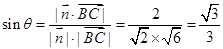 , 11分
, 11分所以
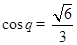
∴直线
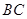 和平面
和平面 所成的角的余弦值为
所成的角的余弦值为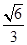 . 12分
. 12分
练习册系列答案
相关题目

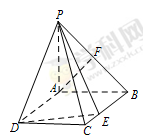
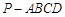 中,底面
中,底面 为矩形,
为矩形,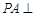 平面
平面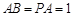 ,
,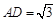 ,
,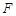 是
是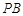 中点,
中点,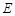 为
为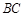 上一点.
上一点.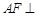 平面
平面 ;
;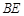 为何值时,二面角
为何值时,二面角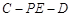 为
为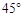 .
.
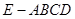 中,底面
中,底面 为正方形,
为正方形,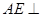 平面
平面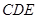 ,已知
,已知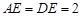 ,
,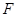 为线段
为线段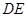 的中点.
的中点.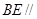 平面
平面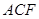 ;
;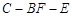 的平面角的余弦值.
的平面角的余弦值.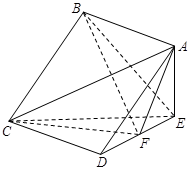
 底面ABCD,
底面ABCD,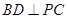 ,E是PA的中点.
,E是PA的中点.
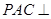 平面EBD;
平面EBD;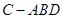 中,
中,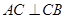 ,
,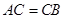 ,
,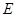 为
为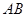 的中点,
的中点,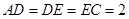 ,
,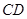 =
=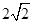 .
.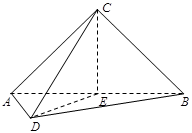
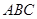 ⊥平面
⊥平面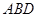 ;
;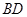 与平面
与平面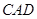 所成角的正弦值.
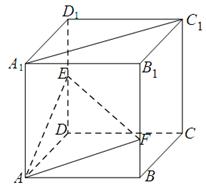
所成角的正弦值.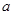 的正方体
的正方体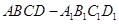 中,点
中,点 是棱
是棱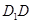 的中点,点
的中点,点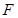 在棱
在棱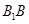 上,且满足
上,且满足 .
.
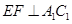 ;
;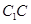 上确定一点
上确定一点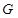 ,使
,使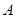 、
、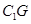 的长;
的长; 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.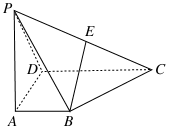
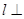 平面
平面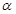 ,直线
,直线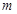
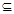 平面
平面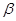 ,给出下列命题,其中正确的是 ( )
,给出下列命题,其中正确的是 ( )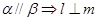 ②
②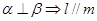
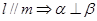 ④
④