题目内容
已知函数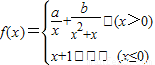 在R上连续,则a-b=( )
在R上连续,则a-b=( )A.2
B.1
C.0
D.-1
【答案】分析:函数f(x)在R上连续,转化成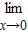 f(x)等于1,建立等式关系,解之即可.
f(x)等于1,建立等式关系,解之即可.
解答:解:∵函数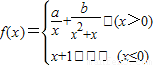 在R上连续
在R上连续
∴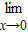
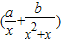 =
=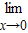
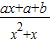 =
=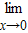 (
(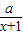 +
+ )=1
)=1
即a=1,a+b=0则b=-1
∴a-b=2
故选A.
点评:本题考查函数的连续性的概念,解题时要正确理解函数的连续性,属于基础题.
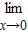 f(x)等于1,建立等式关系,解之即可.
f(x)等于1,建立等式关系,解之即可.解答:解:∵函数
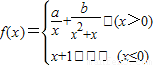 在R上连续
在R上连续∴
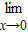
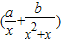 =
=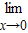
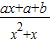 =
=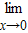 (
(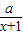 +
+ )=1
)=1即a=1,a+b=0则b=-1
∴a-b=2
故选A.
点评:本题考查函数的连续性的概念,解题时要正确理解函数的连续性,属于基础题.

练习册系列答案
相关题目
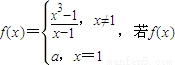 在R上连续,则
在R上连续,则  = .
= .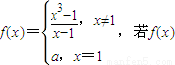 在R上连续,则
在R上连续,则 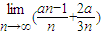 = .
= .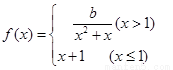 在R上连续,则
在R上连续,则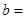 ( )
( )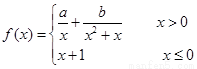 在R上连续,则
在R上连续,则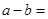 ( )
( )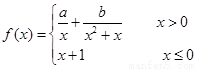 在R上连续,则
在R上连续,则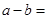 ( )
( )