题目内容
已知函数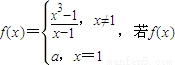 在R上连续,则
在R上连续,则  = .
= .
【答案】分析:本题中函数是一个分段函数,由于函数在xR上连续,故可知函数在点x=1处连续,由其左右两侧函数值的极限相等建立方程求参数,由于其中一段在x=1处无定义,故需要先对其进行变形,以方便判断其右侧函数值的极限.根据极限的运算法则,即可求得结果.
解答:解:当x≠1时,f(x)=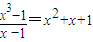
由于函数在x=1处连续,故有
a=1+1+1=3
 =
= (
(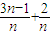 )=
)=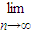 (3+
(3+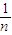 )=3
)=3
故答案为:3.
点评:本题考点是函数的连续性,考查由函数的连续性得到参数的方程求参数,函数连续性的定义是:如果函数在某点处的左极限与右极限相等且等于该点处的函数值,则称此函数在该点处连续.本题中对x≠1时的解析式进行化简是一个难点,变形时要严谨、认真,避免变形出错.属中档题.
解答:解:当x≠1时,f(x)=
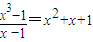
由于函数在x=1处连续,故有
a=1+1+1=3
 =
= (
(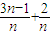 )=
)=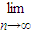 (3+
(3+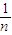 )=3
)=3故答案为:3.
点评:本题考点是函数的连续性,考查由函数的连续性得到参数的方程求参数,函数连续性的定义是:如果函数在某点处的左极限与右极限相等且等于该点处的函数值,则称此函数在该点处连续.本题中对x≠1时的解析式进行化简是一个难点,变形时要严谨、认真,避免变形出错.属中档题.

练习册系列答案
相关题目
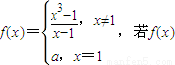 在R上连续,则
在R上连续,则 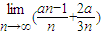 = .
= .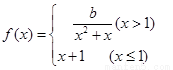 在R上连续,则
在R上连续,则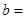 ( )
( )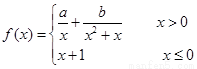 在R上连续,则
在R上连续,则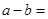 ( )
( )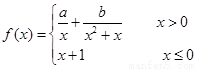 在R上连续,则
在R上连续,则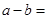 ( )
( )