��Ŀ����
�����У�1������2������3������ѡ���⣬ÿ��7�֣��뿼����ѡ2����������14�֣������������������ǰ����Ʒ֣�����ʱ������2BǦ���ڴ���ϰ���ѡ��Ŀ��Ӧ�����Ϳ�ڣ�����ѡ������������У���1��ѡ��4һ2��������任
�����M����Ӧ�ı任�ǰ�����ƽ���ϵĵ�ĺ������쳤��2�����������쳤��3���������任��
���������M������ֵ����Ӧ������������
�����������M-1�Լ���Բ
 ��M-1�������µ������ߵķ��̣�
��M-1�������µ������ߵķ��̣���2��ѡ��4һ4������ϵ���������
��ֱ֪��
 ��t��������
��t�������� ������������
����������������
 ʱ����C1��C2�Ľ������ꣻ
ʱ����C1��C2�Ľ������ꣻ��������ԭ��O��C1�Ĵ��ߣ�����ΪA��PΪOA�е㣬�����仯ʱ����P��Ĺ켣�IJ������̣�
��3��ѡ��4һ5������ʽѡ��
��֪a��b��c��Ϊ��ʵ������a+b+c=1����
 �����ֵ��
�����ֵ��
���𰸡���������1���������������M��Ȼ��������������ʽ�������������������ֵ�����ֱ��������ֵ����Ӧ������������
�������������M�������Ȼ�����õ��ھ���M-1�������µĵ�����꣬���������Բ��������µ����߷��̣�
��2��������д��C1����ͨ���̺�C2����ͨ����Ϊx2+y2=1�����������鼴�ɽ��C1��C2�Ľ��㣻
����C1����ͨ����Ϊxsin��-ycos��-sin��=0��A������Ϊ��sin2����-cos��sin�������Ӷ��ó������仯ʱ��P��켣�IJ������̼��ɣ�
��3�����ݿ�������ʽ •��4a+1+4b+1+4c+1��ֱ����⼴�ɣ�
•��4a+1+4b+1+4c+1��ֱ����⼴�ɣ�
����⣺�����������þ���M= ��
��
��������ֵΪ2��3����Ӧ����������Ϊ ��
�� ����4�֣�
����4�֣�
����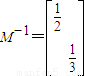 ����Բ
����Բ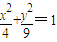 ��M-1�������µ������ߵķ���Ϊx2+y2=1����7�֣�
��M-1�������µ������ߵķ���Ϊx2+y2=1����7�֣�
��2������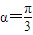 ʱ��C1����ͨ����Ϊ
ʱ��C1����ͨ����Ϊ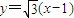 ��
��
C2����ͨ����Ϊx2+y2=1������������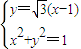 ��
��
���C1��C2�Ľ���Ϊ��1��0����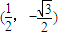 ����4�֣�
����4�֣�
����C1����ͨ����Ϊxsin��-ycos��-sin��=0��A������Ϊ��sin2����-cos��sin������
�ʵ����仯ʱ��P��켣�IJ�������Ϊ��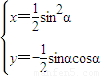 ����Ϊ��������7�֣�
����Ϊ��������7�֣�
��3���ɿ�������ʽ��
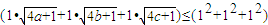 •��4a+1+4b+1+4c+1��
•��4a+1+4b+1+4c+1��
=3[4��a+b+c��+3]=2��15�֣�
���ҽ���a=b=c= ʱ�Ⱥų���
ʱ�Ⱥų���
�� �����ֵΪ
�����ֵΪ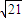 ����7�֣�
����7�֣�
������������Ҫ����������任��������Լ�Բ�IJ������̺�ֱ�ߵIJ������̣��Լ�����ʽ��֤���Ȼ���֪ʶ����һ���ۺ��⣬�����е��⣮
�������������M�������Ȼ�����õ��ھ���M-1�������µĵ�����꣬���������Բ��������µ����߷��̣�
��2��������д��C1����ͨ���̺�C2����ͨ����Ϊx2+y2=1�����������鼴�ɽ��C1��C2�Ľ��㣻
����C1����ͨ����Ϊxsin��-ycos��-sin��=0��A������Ϊ��sin2����-cos��sin�������Ӷ��ó������仯ʱ��P��켣�IJ������̼��ɣ�
��3�����ݿ�������ʽ
 •��4a+1+4b+1+4c+1��ֱ����⼴�ɣ�
•��4a+1+4b+1+4c+1��ֱ����⼴�ɣ�����⣺�����������þ���M=
 ��
����������ֵΪ2��3����Ӧ����������Ϊ
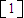 ��
�� ����4�֣�
����4�֣�����
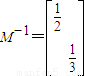 ����Բ
����Բ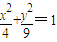 ��M-1�������µ������ߵķ���Ϊx2+y2=1����7�֣�
��M-1�������µ������ߵķ���Ϊx2+y2=1����7�֣���2������
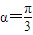 ʱ��C1����ͨ����Ϊ
ʱ��C1����ͨ����Ϊ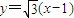 ��
��C2����ͨ����Ϊx2+y2=1������������
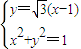 ��
�����C1��C2�Ľ���Ϊ��1��0����
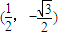 ����4�֣�
����4�֣�����C1����ͨ����Ϊxsin��-ycos��-sin��=0��A������Ϊ��sin2����-cos��sin������
�ʵ����仯ʱ��P��켣�IJ�������Ϊ��
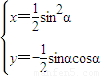 ����Ϊ��������7�֣�
����Ϊ��������7�֣���3���ɿ�������ʽ��
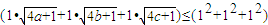 •��4a+1+4b+1+4c+1��
•��4a+1+4b+1+4c+1��=3[4��a+b+c��+3]=2��15�֣�
���ҽ���a=b=c=
 ʱ�Ⱥų���
ʱ�Ⱥų�����
 �����ֵΪ
�����ֵΪ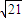 ����7�֣�
����7�֣�������������Ҫ����������任��������Լ�Բ�IJ������̺�ֱ�ߵIJ������̣��Լ�����ʽ��֤���Ȼ���֪ʶ����һ���ۺ��⣬�����е��⣮

��ϰ��ϵ�д�
 ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
�����Ŀ