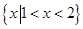题目内容
两个集合A与B之差记作“A/B”,定义A/B={x|x∈A,且x∉B },如果集合A={x|0<x<2},B={ x|-1<x-2<1},则A/B=
{x|0<x≤3}
{x|0<x≤3}
.分析:由题意通过解不等式求出集合B,利用新定义直接求出A/B即可.
解答:解:集合B={ x|-1<x-2<1}={x|1<x<3}
因为两个集合A与B之差记作“A/B”,定义为:A/B={x|x∈A,且x∉B},那么A/B={x|0<x≤1}.
故答案为:{x|0<x≤1}.
因为两个集合A与B之差记作“A/B”,定义为:A/B={x|x∈A,且x∉B},那么A/B={x|0<x≤1}.
故答案为:{x|0<x≤1}.
点评:本题是中档题,正确利用新定义,求出集合的解集是解题的关键,考查计算能力.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
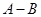 ” 定义为
” 定义为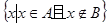 ,若集合
,若集合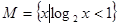 ,N=
,N=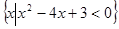 ,则
,则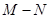 等于( )
等于( )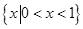 B.
B.
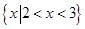 D.
D.