题目内容
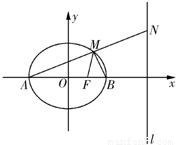
如图,已知椭圆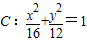 的左、右顶点分别为A、B,右焦点为F,直线l为椭圆的右准线,N为l上一动点,且在x轴上方,直线AN与椭圆交于点M.
的左、右顶点分别为A、B,右焦点为F,直线l为椭圆的右准线,N为l上一动点,且在x轴上方,直线AN与椭圆交于点M.(1)若AM=MN,求∠AMB的余弦值;
(2)设过A,F,N三点的圆与y轴交于P,Q两点,当线段PQ的中点坐标为(0,9)时,求这个圆的方程.
【答案】分析:(1)根据统一可知直线l的方程,设N(8,t)(t>0),因为AM=MN,所以M(2, ),由M在椭圆上,得t=6.可求出点M的坐标,求出向量
),由M在椭圆上,得t=6.可求出点M的坐标,求出向量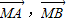 ,然后利用向量的夹角公式进行求解即可;
,然后利用向量的夹角公式进行求解即可;
(2)设圆的方程为x2+y2+Dx+Ey+F=0,将A,F,N三点坐标代入,即可求出圆的方程,令x=0,得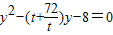 ,最后根据线段PQ的中点坐标为(0,9),
,最后根据线段PQ的中点坐标为(0,9),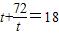 求出t,从而求出圆的方程.
求出t,从而求出圆的方程.
解答:解:(1)由已知,A(-4,0),B(4,0),F(2,0),直线l的方程为x=8.
设N(8,t)(t>0),因为AM=MN,所以M(2, ).
).
由M在椭圆上,得t=6.故所求的点M的坐标为M(2,3).(4分)
所以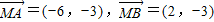 ,
,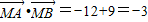 .
.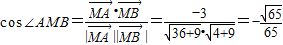 .(7分)
.(7分)
(2)设圆的方程为x2+y2+Dx+Ey+F=0,将A,F,N三点坐标代入,
得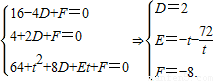
∵圆方程为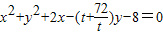 ,令x=0,得
,令x=0,得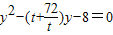 .(11分)
.(11分)
设P(0,y1),Q(0,y2),则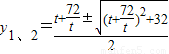 .
.
由线段PQ的中点坐标为(0,9),得y1+y2=18,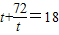 .
.
此时所求圆的方程为x2+y2+2x-18y-8=0.(15分)
点评:本题主要考查了椭圆的性质以及利用向量法求夹角,同时考查了圆的方程,分析问题解决问题的能力,属于中档题.
 ),由M在椭圆上,得t=6.可求出点M的坐标,求出向量
),由M在椭圆上,得t=6.可求出点M的坐标,求出向量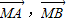 ,然后利用向量的夹角公式进行求解即可;
,然后利用向量的夹角公式进行求解即可;(2)设圆的方程为x2+y2+Dx+Ey+F=0,将A,F,N三点坐标代入,即可求出圆的方程,令x=0,得
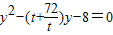 ,最后根据线段PQ的中点坐标为(0,9),
,最后根据线段PQ的中点坐标为(0,9),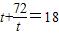 求出t,从而求出圆的方程.
求出t,从而求出圆的方程.解答:解:(1)由已知,A(-4,0),B(4,0),F(2,0),直线l的方程为x=8.
设N(8,t)(t>0),因为AM=MN,所以M(2,
 ).
).由M在椭圆上,得t=6.故所求的点M的坐标为M(2,3).(4分)
所以
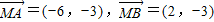 ,
,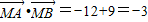 .
.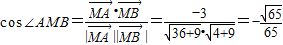 .(7分)
.(7分)(2)设圆的方程为x2+y2+Dx+Ey+F=0,将A,F,N三点坐标代入,
得
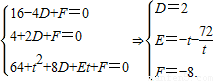
∵圆方程为
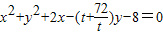 ,令x=0,得
,令x=0,得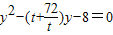 .(11分)
.(11分)设P(0,y1),Q(0,y2),则
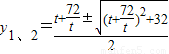 .
.由线段PQ的中点坐标为(0,9),得y1+y2=18,
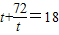 .
.此时所求圆的方程为x2+y2+2x-18y-8=0.(15分)
点评:本题主要考查了椭圆的性质以及利用向量法求夹角,同时考查了圆的方程,分析问题解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在平面直角坐标系
在平面直角坐标系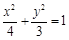 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
 ,求直线AB的斜率;
,求直线AB的斜率; 的左、右焦点分别为
的左、右焦点分别为 ,下顶点为
,下顶点为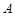 ,点
,点 是椭圆上任一点,圆
是椭圆上任一点,圆 是以
是以 为直径的圆.
为直径的圆. ,求
,求 所在的直线方程;
所在的直线方程; 相切时,求圆
相切时,求圆
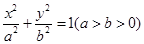 的左顶点为
的左顶点为 ,左焦点为
,左焦点为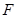 ,上顶点为
,上顶点为 ,若
,若 ,则该椭圆的离心率是
.
,则该椭圆的离心率是
.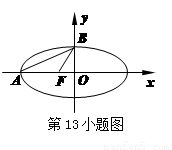
 的左、右准线分别为l1、l2,且分别交x轴于C、D两点,从l1上一点A发出一条光线经过椭圆的左焦点F被x轴反射后与l2交于点B,若
的左、右准线分别为l1、l2,且分别交x轴于C、D两点,从l1上一点A发出一条光线经过椭圆的左焦点F被x轴反射后与l2交于点B,若 ,且
,且 ,则椭圆的离心率等于_____________.
,则椭圆的离心率等于_____________.