题目内容
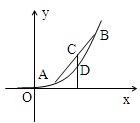 设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).
设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).(1)若
| AC |
| CB |
(2)过点C作x轴的垂线,交函数y=x2(x>0)的图象于D点,由点C在点D的上方可得不等式:
分析:(1)由A(a,a2),B(b,b2),将A,B两点的坐标代入定比分点坐标公式:坐标公式
,易得分点C的坐标.
(2)结合题目中给出的图象,分析C、D两点的位置关系,由于D在函数图象上,故也不难得到D点的坐标,再结合C、D两点的坐标不难得到相应的不等式.
|
(2)结合题目中给出的图象,分析C、D两点的位置关系,由于D在函数图象上,故也不难得到D点的坐标,再结合C、D两点的坐标不难得到相应的不等式.
解答:解:(1)设点C(x,y),因为点A(a,a2),B(b,b2),
=λ
,
则(x-a,y-a2)=λ(b-x,b2-y),
所以:x=
,y=
(2)因为点C在点D的上方,
则y>yD,所以
>(
)2
| AC |
| CB |
则(x-a,y-a2)=λ(b-x,b2-y),
所以:x=
| a+λb |
| 1+λ |
| a2+λb2 |
| 1+λ |
(2)因为点C在点D的上方,
则y>yD,所以
| a2+λb2 |
| 1+λ |
| a+λb |
| 1+λ |
点评:如果已知,有向线段A(x1,y1),B(x2,y2).及点C分线段AB所成的比,求分点C的坐标,可将A,B两点的坐标代入定比分点坐标公式:坐标公式
进行求解.
|

练习册系列答案
相关题目
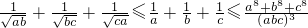 .
. 的最小值为( )
的最小值为( )

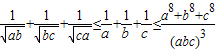 .
.