题目内容
设x1,x2是函数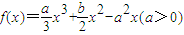 的两个极值点,且|x1-x2|=2.
的两个极值点,且|x1-x2|=2.(Ⅰ)证明:0<a≤1;
(Ⅱ)证明:
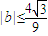 .
.
【答案】分析:(I)对函数求导可得,f′(x)=ax2+bx-a2,由题意可得x1,x2是方程的两根,根据方程的根与系数的关系可得x1+x2,x1•x2,而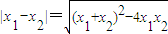 ,代入可求
,代入可求
(II)由(I)可得b2=4a2-4a3,构造函数g(a)=4a2-4a3,利用导数知识求函数g(a)的单调区间及最值,而b2≤g(a)max,即可.
解答:解:(Ⅰ)对f(x)求导可得f'(x)=ax2+bx-a2(a>0).(2分)
因为x1,x2是f(x)的两个极值点,所以x1,x2是方程f'(x)=0的两个实根.
于是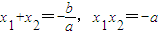 ,
,
故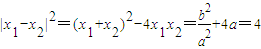 ,
,
即b2=4a2-4a3.(4分)
由b2≥0得4a2-4a3≥0,解得a≤1.a>0,
所以0<a≤1得证.(6分)
(Ⅱ)由(Ⅰ)知b2=4a2-4a3,设g(a)=4a2-4a3,
则g'(a)=8a-12a2=4a(2-3a).(8分)
由g'(a)>0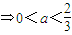 ;g'(a)<0
;g'(a)<0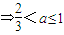 .(10分)
.(10分)
故g(a)在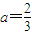 时取得最大值
时取得最大值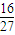 ,
,
即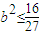 ,
,
所以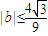 .(13分)
.(13分)
点评:本题是函数的导数的简单运用,熟练运用导数的知识解决问题,要求考生熟练掌握基本知识,灵活转化问题,还要具备一定的逻辑推理的能力.
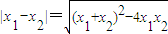 ,代入可求
,代入可求(II)由(I)可得b2=4a2-4a3,构造函数g(a)=4a2-4a3,利用导数知识求函数g(a)的单调区间及最值,而b2≤g(a)max,即可.
解答:解:(Ⅰ)对f(x)求导可得f'(x)=ax2+bx-a2(a>0).(2分)
因为x1,x2是f(x)的两个极值点,所以x1,x2是方程f'(x)=0的两个实根.
于是
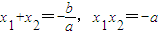 ,
,故
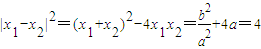 ,
,即b2=4a2-4a3.(4分)
由b2≥0得4a2-4a3≥0,解得a≤1.a>0,
所以0<a≤1得证.(6分)
(Ⅱ)由(Ⅰ)知b2=4a2-4a3,设g(a)=4a2-4a3,
则g'(a)=8a-12a2=4a(2-3a).(8分)
由g'(a)>0
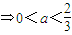 ;g'(a)<0
;g'(a)<0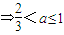 .(10分)
.(10分)故g(a)在
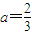 时取得最大值
时取得最大值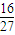 ,
,即
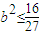 ,
,所以
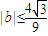 .(13分)
.(13分)点评:本题是函数的导数的简单运用,熟练运用导数的知识解决问题,要求考生熟练掌握基本知识,灵活转化问题,还要具备一定的逻辑推理的能力.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
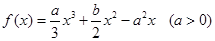 的两个极值点,且
的两个极值点,且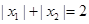 。
。 ,并求出a的取值范围.
,并求出a的取值范围.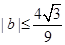 .
.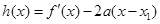 ,证明:当
,证明:当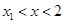 且x1<0时,
且x1<0时, 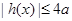 .
.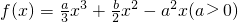 的两个极值点,且|x1|+|x2|=2.
的两个极值点,且|x1|+|x2|=2.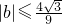 .
.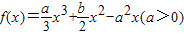 的两个极值点,且|x1-x2|=2.
的两个极值点,且|x1-x2|=2. .
.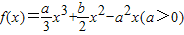 的两个极值点,且|x1-x2|=2.
的两个极值点,且|x1-x2|=2.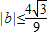 .
.