题目内容
10.已知tanα是关于x的方程2x2-x-1=0的一个实根,且α是第三象限角.(1)求$\frac{2sinα-cosα}{sinα+cosα}$的值;
(2)求cosα+sinα的值.
分析 (1)利用已知条件求出正切函数值,化简所求表达式为正切函数的形式,计算即可.
(2)利用同角三角函数的基本关系式,通过解方程求解即可.
解答 解:∵2x2-x-1=0,∴${x_1}=-\frac{1}{2},{x_2}=1$,∴$tanα=-\frac{1}{2}$或tanα=1,又α是第三象限角,…(4分)
(1)$\frac{2sinα-cosα}{sinα+cosα}=\frac{2tanα-1}{tanα+1}=\frac{2×1-1}{1+1}=\frac{1}{2}$.…(9分)
(2)∵$\left\{\begin{array}{l}tanα=\frac{sinα}{cosα}=1\\{sin^2}α+{cos^2}α=1\end{array}\right.$且α是第三象限角,∴$\left\{\begin{array}{l}sinα=-\frac{{\sqrt{2}}}{2}\\ cosα=-\frac{{\sqrt{2}}}{2}\end{array}\right.$,∴$sinα+cosα=-\sqrt{2}$…(14分)
点评 本题考查三角函数的化简求值,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
相关题目
20.已知函数f(x)=$\frac{\sqrt{4-{x}^{2}}}{|x+3|-3}$,若f(a)=$\frac{5\sqrt{7}}{3}$,则f(-a)=( )
| A. | $\frac{5\sqrt{7}}{3}$ | B. | -$\frac{5\sqrt{7}}{3}$ | C. | 2$\sqrt{7}$ | D. | 4$\sqrt{7}$ |
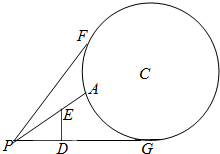 如图,地面上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高为10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧.
如图,地面上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高为10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧.