题目内容
6.圆x2+y2=4被直线$\sqrt{3}x+y-2\sqrt{3}$=0截得的弦长为( )| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | 2 |
分析 求出圆的圆心到直线的距离,利用圆心距、半径、半弦长满足勾股定理,求出半弦长,然后求出弦长.
解答 解:圆心到直线的距离为:$\frac{|-2\sqrt{3}|}{\sqrt{3+1}}$=$\sqrt{3}$.
圆的半径为2,所以半弦长为:$\sqrt{4-3}$=1.
所以圆x2+y2=4被直线$\sqrt{3}x+y-2\sqrt{3}$=0截得的弦长为2.
故选:D.
点评 本题考查直线与圆的位置关系,注意圆心距与半径和弦长的关系,考查计算能力.

练习册系列答案
相关题目
1.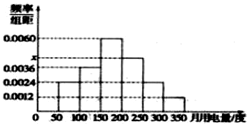 利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )
利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )
 利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )
利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
16.函数f(x)=cos(2x-$\frac{π}{4}$)在区间[0,$\frac{π}{2}$]上的最小值为( )
| A. | -1 | B. | -$\frac{\sqrt{2}}{2}$ | C. | 0 | D. | $\frac{\sqrt{2}}{2}$ |
 已知斜四棱柱ABCD-A1B1C1D1的底面是矩形,侧面CC1D1D垂直底面ABCD,BC=2AB=DC1=2,BD1=2$\sqrt{3}$
已知斜四棱柱ABCD-A1B1C1D1的底面是矩形,侧面CC1D1D垂直底面ABCD,BC=2AB=DC1=2,BD1=2$\sqrt{3}$
 如图,延长△ABC的角平分线AD交其外接圆于E,若AD=AB=1,DE=$\sqrt{2}$,则AC=$\sqrt{2}+1$.
如图,延长△ABC的角平分线AD交其外接圆于E,若AD=AB=1,DE=$\sqrt{2}$,则AC=$\sqrt{2}+1$.