题目内容
设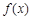
是定义在R上的奇函数，且当
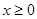时，
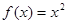，若对任意的
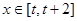，不等式
恒成立，则实数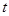
的取值范围是 ．
【答案】
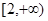
【解析】因为当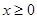
时，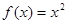
，因为函数是奇函数，故当x<0是，-x>0，f(-x)=-f(x)=x2,即f(x)=-x2.那么可知函数在R上式单调函数，因此可知，
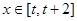，不等式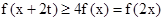
恒成立等价于x+2t
,恒成立， 得到实数t的范围是
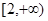
练习册系列答案
阅读快车系列答案
相关题目
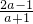，则a的取值范围是________．
，则a的取值范围是 ．