题目内容
(理)斜率为1的直线过抛物线y2=2px(p>0)的焦点,且与抛物线交于两点A、B.
(1)若p=2,求|AB|的值;
(2)将直线AB按向量
=(-p,0)平移得直线m,N是m上的动点,求
•
的最小值.
(3)设C(p,0),D为抛物线y2=2px(p>0)上一动点,是否存在直线l,使得l被以CD为直径的圆截得的弦长恒为定值?若存在,求出l的方程;若不存在,说明理由.
(1)若p=2,求|AB|的值;
(2)将直线AB按向量
| a |
| NA |
| NB |
(3)设C(p,0),D为抛物线y2=2px(p>0)上一动点,是否存在直线l,使得l被以CD为直径的圆截得的弦长恒为定值?若存在,求出l的方程;若不存在,说明理由.
(1)设A(x1,y1),B(x2,y2),p=2时,直线AB:y=x-1,代入y2=4x中
可得:x2-6x+1=0(2分)
则x1+x2=6,由定义可得:|AB|=x1+x2+p=8.(4分)
(2)直线AB:y=x-
,代入y2=2px(p>0)中,可得:x2-3px+
p2=0
则x1+x2=3p,x1x2=
,设N(x0,x0+
),
则
=(x1-x0,y1-x0-
),
=(x2-x0,y2-x0-
)
即
•
=x1x2-x0(x1+x2)+
+y1y2-(x0+
)(y1+y2)+(x0+
)2(2分)
由x1+x2=3p,x1x2=
,y1y2=-p2,y1+y2=2p(4分)
则
•
=2
-4px0-
p2=2(x0-p)2-
p2
当x0=p时,
•
的最小值为-
p2. (6分)
(3)假设满足条件的直线l存在,其方程为x=a,
设CD的中点为O',l与以CD为直径的圆相交于点P、Q,设PQ的中点为H,
则O'H⊥PQ,O'点的坐标为(
,
).
∵|O′P|=
|CD|=
=
,
|O′H|=|a-
|=
|2a-x1-p|,(2分)
∴|PH|2=|O'P|2-|O'H|2=
(
+p2)-
(2a-x1-p)2=(a-
)x1+a(p-a),
∴|PQ|2=(2|PH|)2=4[(a-
)x1+a(p-a)]. (5分)
令a-
=0,得a=
,此时|PQ|=p为定值,
故满足条件的直线l存在,其方程为x=
,即抛物线的通径所在的直线. (7分)
可得:x2-6x+1=0(2分)
则x1+x2=6,由定义可得:|AB|=x1+x2+p=8.(4分)
(2)直线AB:y=x-
| p |
| 2 |
| 1 |
| 4 |
则x1+x2=3p,x1x2=
| p2 |
| 4 |
| p |
| 2 |
则
| NA |
| p |
| 2 |
| NB |
| p |
| 2 |
即
| NA |
| NB |
| x | 20 |
| p |
| 2 |
| p |
| 2 |
由x1+x2=3p,x1x2=
| p2 |
| 4 |
则
| NA |
| NB |
| x | 20 |
| 3 |
| 2 |
| 7 |
| 2 |
当x0=p时,
| NA |
| NB |
| 7 |
| 2 |
(3)假设满足条件的直线l存在,其方程为x=a,
设CD的中点为O',l与以CD为直径的圆相交于点P、Q,设PQ的中点为H,
则O'H⊥PQ,O'点的坐标为(
| x1+p |
| 2 |
| y1 |
| 2 |
∵|O′P|=
| 1 |
| 2 |
| 1 |
| 2 |
(
|
| 1 |
| 2 |
|
|O′H|=|a-
| x1+p |
| 2 |
| 1 |
| 2 |
∴|PH|2=|O'P|2-|O'H|2=
| 1 |
| 4 |
| x | 21 |
| 1 |
| 4 |
| p |
| 2 |
∴|PQ|2=(2|PH|)2=4[(a-
| p |
| 2 |
令a-
| p |
| 2 |
| p |
| 2 |
故满足条件的直线l存在,其方程为x=
| p |
| 2 |

练习册系列答案
相关题目
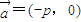 平移得直线m,N是m上的动点,求
平移得直线m,N是m上的动点,求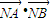 的最小值.
的最小值.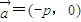 平移得直线m,N是m上的动点,求
平移得直线m,N是m上的动点,求 的最小值.
的最小值.