题目内容
如图,在长方体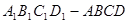 中,
中,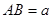 ,
,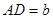 ,
,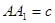 ,
,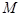 是线段
是线段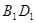 的中点.
的中点.
(Ⅰ)求证: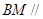 平面
平面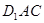 ;
;
(Ⅱ)求平面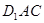 把长方体
把长方体
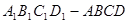 分成的两部分的体积比.
分成的两部分的体积比.

【答案】
(Ⅰ)详见解析;(Ⅱ) 或
或 .
.
【解析】
试题分析:1. 第(Ⅰ)问有一点难度,需要作辅助线,这几乎是用几何法证明线面平行、线面垂直的必经之路了,对此考生要有意识.2.第(Ⅱ)问的解决比较简单,并且不依赖于第(Ⅰ)问,有的考生第(Ⅰ)问没有做出来,但第(Ⅱ)问做出来了,这是一种好的现象,说明考生能够把会做的做对了.
试题解析:(Ⅰ)证明:设 的中点为
的中点为 ,连接
,连接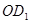 ,
, .
.

根据题意得 ,
, 
 ,且
,且
 .
.
∴四边形 是平行四边形.
是平行四边形.
∴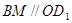 .
.
∵ 平面
平面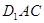 ,
, 平面
平面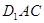 ,
,
∴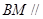 平面
平面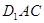 .
.
(Ⅱ)解:∵ ,
,
 ,
,
∴空间几何体 的体积
的体积

 .
.
∴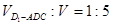 或
或 ,即平面
,即平面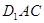 把长方体
把长方体
 分成的两部分的体积比为
分成的两部分的体积比为 或
或 .
.
考点:空间线面位置关系,线面平行,三棱锥体积的求法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在长方体中,
如图,在长方体中,


 中,
中, ,
, 则
则 与平面
与平面 所成角的正弦值为 ( )
所成角的正弦值为 ( )
 B.
B. C.
C. D.
D.