题目内容
给出问题:F1、F2是双曲线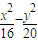 =1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
=1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.该学生的解答是否正确?若正确,请将他的解题依据填在下面空格内,若不正确,将正确的结果填在下面空格内 .
【答案】分析:看当|PF2|=1时△PF1F2两边之差大于第三边,与三角形两边之差小于第三边的性质矛盾.进而可判断学生的解答不正确.
解答:解:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
依题意知|F1F2|=12,若|PF2|=1,
由题设|PF1|=9知△PF1F2两边之差大于第三边,与三角形两边之差小于第三边的性质矛盾.
故学生解答不正确.
故答案为|PF2|=17.
点评:本题主要考查了双曲线的简单性质.解决此类问题,需要在复习过程中注意对思维的严谨性和推理的逻辑性进行训练,也要注意对课本、参考书和教师同学的解法进行反思和加工,从而形成良好的批判思维能力
解答:解:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
依题意知|F1F2|=12,若|PF2|=1,
由题设|PF1|=9知△PF1F2两边之差大于第三边,与三角形两边之差小于第三边的性质矛盾.
故学生解答不正确.
故答案为|PF2|=17.
点评:本题主要考查了双曲线的简单性质.解决此类问题,需要在复习过程中注意对思维的严谨性和推理的逻辑性进行训练,也要注意对课本、参考书和教师同学的解法进行反思和加工,从而形成良好的批判思维能力

练习册系列答案
相关题目
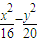 =1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
=1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.