题目内容
(本小题满分12分)2010年广东亚运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
乙系列:
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I) 若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(II) (II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
甲系列:
| 动作 | K | D | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 | 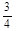 | 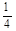 | 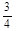 | 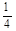 |
| 动作 | K | D | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 | 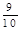 | 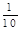 | 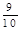 | 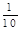 |
(I) 若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(II) (II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
【解】(I)若该运动员希望获得该项目的第一名,应选择甲系列.……1分
理由如下:选择甲系列最高得分为100+40=140>118,可能获得第一名;而选择乙系列最高得分为90+20=110<118,不可能获得第一名. ……2分
记“该运动员完成K动作得100分”为事件A,“该运动员完成D动作得40分”为事件B,则P (A)=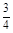 ,P (B)=
,P (B)=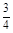 . 4分
. 4分
记“该运动员获得第一名”为事件C,依题意得P(C)=P(AB)+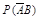 =
=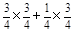 =
=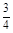 .
.
该运动员获得第一名的概率为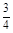 .…………6分
.…………6分
(II)若该运动员选择乙系列,X的可能取值是50,70,90,110
则P (X=50)=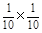 =
=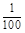 , P (X=70)=
, P (X=70)= =
=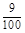 ,P (X=90)=
,P (X=90)=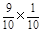 =
=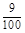 , P (X=110)=
, P (X=110)=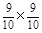 =
=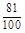 .……9分
.……9分
X的分布列为:
∴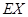 =50×
=50×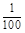 +70×
+70×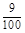 +90×
+90×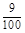 +110×
+110×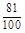 =104. ……12分
=104. ……12分
理由如下:选择甲系列最高得分为100+40=140>118,可能获得第一名;而选择乙系列最高得分为90+20=110<118,不可能获得第一名. ……2分
记“该运动员完成K动作得100分”为事件A,“该运动员完成D动作得40分”为事件B,则P (A)=
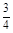 ,P (B)=
,P (B)=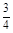 . 4分
. 4分记“该运动员获得第一名”为事件C,依题意得P(C)=P(AB)+
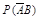 =
=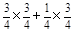 =
=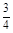 .
.该运动员获得第一名的概率为
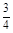 .…………6分
.…………6分(II)若该运动员选择乙系列,X的可能取值是50,70,90,110
| X | 50 | 70 | 90 | 110 |
| P | 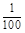 | 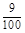 | 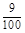 | 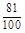 |
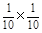 =
=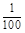 , P (X=70)=
, P (X=70)= =
=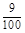 ,P (X=90)=
,P (X=90)=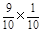 =
=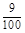 , P (X=110)=
, P (X=110)=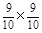 =
=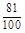 .……9分
.……9分X的分布列为:
∴
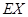 =50×
=50×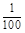 +70×
+70×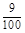 +90×
+90×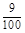 +110×
+110×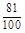 =104. ……12分
=104. ……12分略

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
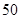 名学生的成绩进行统计分析.
名学生的成绩进行统计分析.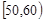

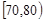
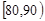
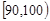

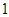 )班和(
)班和(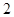 )班报名参加的人数分别是
)班报名参加的人数分别是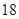 和
和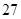 .现用分层抽样的方法,从中抽取若干名学生组成研究性学习小组,已知从(
.现用分层抽样的方法,从中抽取若干名学生组成研究性学习小组,已知从(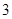 名同学.
名同学.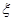 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求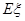 .
.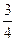 是境外游客,其余是境内游客。在境外游客中有
是境外游客,其余是境内游客。在境外游客中有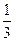 持金卡,在境内游客中有
持金卡,在境内游客中有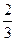 持银卡
持银卡 团的省内游客中随机采访3名
团的省内游客中随机采访3名 游客,设其中持银卡人数为随机变量
游客,设其中持银卡人数为随机变量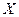 ,求
,求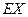
 ,
, ,
, ,某次全市20000人参加的考试,数学成绩大致服从正态分布
,某次全市20000人参加的考试,数学成绩大致服从正态分布 ,则本次考试120分以上的学生约有 人.
,则本次考试120分以上的学生约有 人.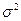 ),若P(ξ>2)=0.023,则P(-2
),若P(ξ>2)=0.023,则P(-2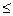 ξ
ξ