题目内容
若椭圆C的中心在原点,焦点在x轴上,短轴的一个端点与左右焦点F1、F2组成一个正三角形,焦点到椭圆上的点的最短距离为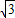 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)过点F2作直线l与椭圆C交于A、B两点,线段AB的中点为M,求直线MF1的斜率k的取值范围.
【答案】分析:(1)设出椭圆的标准方程,进而根据题设的条件组成方程组求得a和b,则椭圆的方程可得.
(2)当直线l的斜率不存在时,AB的中点为F2,直线MF1的斜率k=0;当直线l的斜率存在时,设其斜率为m,直线AB的方程可知,与椭圆方程联立消去y,设M(x,y),进而可表示出x和y,当m=0时,AB的中点为坐标原点,直线MF1的斜率k=0;当m≠0时用x和y表示斜率,进而根据m的范围确定k的范围.综合答案可得.
解答:解:(Ⅰ)设椭圆C的方程为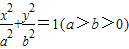
由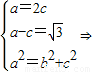
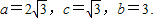
所以,椭圆C的方程为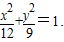
(Ⅱ)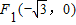 、
、 ,
,
当直线l的斜率不存在时,AB的中点为F2,
直线MF1的斜率k=0;
当直线l的斜率存在时,设其斜率为m,
直线AB的方程为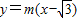 ,
,
由椭圆方程联立消去y并整理得: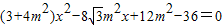
设M(x,y),则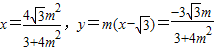
当m=0时,AB的中点为坐标原点,直线MF1的斜率k=0;
当m≠0时,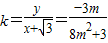 ,
,
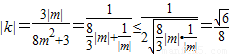
∴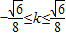 且k≠0.
且k≠0.
综上所述,直线MF1的斜率k的取值范围是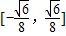 .
.
点评:本题主要考查了椭圆的标准方程和椭圆与直线的关系.考查了学生综合分析问题和解决问题的能力.
(2)当直线l的斜率不存在时,AB的中点为F2,直线MF1的斜率k=0;当直线l的斜率存在时,设其斜率为m,直线AB的方程可知,与椭圆方程联立消去y,设M(x,y),进而可表示出x和y,当m=0时,AB的中点为坐标原点,直线MF1的斜率k=0;当m≠0时用x和y表示斜率,进而根据m的范围确定k的范围.综合答案可得.
解答:解:(Ⅰ)设椭圆C的方程为
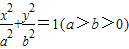
由
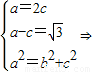
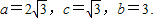
所以,椭圆C的方程为
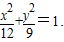
(Ⅱ)
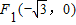 、
、 ,
,当直线l的斜率不存在时,AB的中点为F2,
直线MF1的斜率k=0;
当直线l的斜率存在时,设其斜率为m,
直线AB的方程为
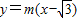 ,
,由椭圆方程联立消去y并整理得:
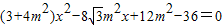
设M(x,y),则
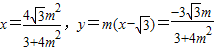
当m=0时,AB的中点为坐标原点,直线MF1的斜率k=0;
当m≠0时,
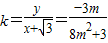 ,
,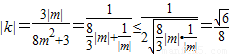
∴
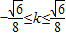 且k≠0.
且k≠0.综上所述,直线MF1的斜率k的取值范围是
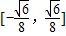 .
.点评:本题主要考查了椭圆的标准方程和椭圆与直线的关系.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
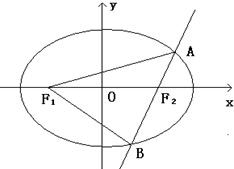 已知椭圆C的中心在原点,焦点F1,F2在x轴上,离心率
已知椭圆C的中心在原点,焦点F1,F2在x轴上,离心率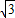 .
.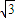 .
.