题目内容
 已知椭圆C的中心在原点,焦点F1,F2在x轴上,离心率e=
已知椭圆C的中心在原点,焦点F1,F2在x轴上,离心率e=
| ||
| 2 |
| 2 |
(1)求椭圆C的方程;
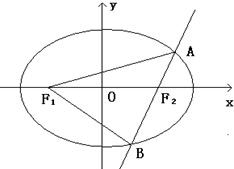
(2)若直线l经过椭圆C的右焦点F2,且与椭圆C交于A,B两点,使得|F1A|,|AB|,|BF1|依次成等差数列,求直线l的方程.
分析:(1)先设椭圆C的方程根据离心率和点M求得a和b,进而可得答案.
(2)设直线l的方程为y=k(x-
),代入(1)中所求的椭圆C的方程,消去y,设A(x1,y1),B(x2,y2),进而可得到x1+x2和x1•x2的表达式,根据F1A|+|BF1|=2|AB|求得k,再判断直线l⊥x轴时,直线方程不符合题意.最后可得答案.
(2)设直线l的方程为y=k(x-
| 2 |
解答:解:(1)设椭圆C的方程为
+
=1,(其中a>b>0)
由题意得e=
=
,且
+
=1,解得a2=4,b2=2,c2=2,
所以椭圆C的方程为
+
=1.
(2)设直线l的方程为y=k(x-
),代入椭圆C的方程
+
=1,
化简得(2+4k2)x2-8
k2x+8k2-8=0,
设A(x1,y1),B(x2,y2),则x1+x2=
,x1•x2=
,
由于|F1A|,|AB|,|BF1|依次成等差数列,则|F1A|+|BF1|=2|AB|.
而|F1A|+|AB|+|BF1|=4a=8,所以|AB|=
.|AB|=
|x1-x2|=
•
=
=
=
,解得k=±1;
当直线l⊥x轴时,x=
,代入得y=±1,|AB|=2,不合题意.
所以,直线l的方程为y=±(x-
).
| x2 |
| a2 |
| y2 |
| b2 |
由题意得e=
| c |
| a |
| ||
| 2 |
| 2 |
| a2 |
| 1 |
| b2 |
所以椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 2 |
(2)设直线l的方程为y=k(x-
| 2 |
| x2 |
| 4 |
| y2 |
| 2 |
化简得(2+4k2)x2-8
| 2 |
设A(x1,y1),B(x2,y2),则x1+x2=
8
| ||
| 2+4k2 |
| 8k2-8 |
| 2+4k2 |
由于|F1A|,|AB|,|BF1|依次成等差数列,则|F1A|+|BF1|=2|AB|.
而|F1A|+|AB|+|BF1|=4a=8,所以|AB|=
| 8 |
| 3 |
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
4
| ||
| 1+2k2 |
| 4(1+k2) |
| 1+2k2 |
| 8 |
| 3 |
当直线l⊥x轴时,x=
| 2 |
所以,直线l的方程为y=±(x-
| 2 |
点评:本题主要考查了椭圆的标准方程和椭圆与其他曲线的关系.要求学生综合掌握如直线、椭圆、抛物线等圆锥曲线的基本性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 。
。