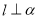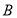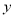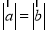题目内容
平面直角坐标系中, 为原点,射线
为原点,射线 与
与 轴正半轴重合,射线
轴正半轴重合,射线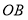 是第一象限角平分线.在
是第一象限角平分线.在 上有点列
上有点列 ,
, ,在
,在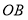 上有点列
上有点列 ,
, ,
, .已知
.已知 ,
, ,
,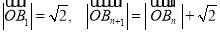 .
.

(1)求点 的坐标;
的坐标;
(2)求 的坐标;
的坐标;
(3)求 面积的最大值,并说明理由.
面积的最大值,并说明理由.
(1) ,
, ; (2)
; (2) ,
, ;(3)
;(3) ;
;
【解析】
试题分析:(1)由 和
和 可求
可求 ,由射线
,由射线 是第一象限角平分线和
是第一象限角平分线和 ,利用向量模的公式可求
,利用向量模的公式可求 ;(2)设
;(2)设 ,
, 可得
可得
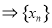 成等比数列,又
成等比数列,又 得
得 ,进而得到
,进而得到 ;设
;设 ,得
,得 ,由
,由 ,得
,得 得
得 是等差数列,可求得
是等差数列,可求得 ,进而求得
,进而求得 ;(3)由
;(3)由 ,可得
,可得 ,利用换元法设
,利用换元法设 ,当
,当 时,
时, 可知
可知 时,
时, 是递增数列,
是递增数列, 时,
时, 是递减数列,即
是递减数列,即 进而求得
进而求得 ;
;
试题解析:(1) ,
,  , 2分
, 2分
设 ,由
,由 ,
,
 ,∴
,∴  ; 4分
; 4分
(2)设 ,则
,则 ,
,
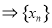 成等比数列, 5分
成等比数列, 5分
 ,∴
,∴  ; 6分
; 6分
设 ,
, , 7分
, 7分
由 ,
,
∴ 是等差数列, 8分
是等差数列, 8分
 , ∴
, ∴  . 9分
. 9分
(3) , 11分
, 11分
设 ,
,
当 时,
时,
 , 12分
, 12分
∴ 时,
时, 是递增数列,
是递增数列, 时,
时, 是递减数列,
是递减数列,
 , 13分
, 13分
∴ . 14分
. 14分
考点:1.向量的坐标表示;2等差、等比数列的通项公式;3.数列的增减性.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目