题目内容
(1)求右焦点坐标是(2,0),且经过点(-2,-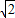 )的椭圆的标准方程.
)的椭圆的标准方程.(2)已知椭圆C的方程是
 +
+ =1(a>b>0).设斜率为k的直线l交椭圆C于A、B两点,AB的中点为M.证明:当直线l平行移动时,动点M在一条过原点的定直线上.
=1(a>b>0).设斜率为k的直线l交椭圆C于A、B两点,AB的中点为M.证明:当直线l平行移动时,动点M在一条过原点的定直线上.(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.

【答案】分析:(1)先设出椭圆的标准方程,根据焦点坐标可求得c,进而可得a和b的关系,把点(-2,- )代入椭圆方程,求得b,进而根据a=
)代入椭圆方程,求得b,进而根据a= 求得a,椭圆的方程可得.
求得a,椭圆的方程可得.
(2)设直线l的方程为y=kx+m且椭圆C的交点A(x1,y1)、B(x2,y2),直线方程和椭圆方程联立进而可得x1+x2和y1+y2的表达式,进而可得AB中点M的坐标进而可判定AB的中点M在过原点的直线b2x+a2ky=0上.
(3)作两条平行直线分别交椭圆于A、B和C、D,并分别取AB、CD的中点M、N,连接直线MN;又作两条平行直线(与前两条直线不平行)分别交椭圆于A1、B1和C1、D1,并分别取A1B1、C1D1的中点M1、N1,连接直线M1N1,那么直线MN和M1N1的交点O即为椭圆中心.
解答: 解:(1)设椭圆的标准方程为
解:(1)设椭圆的标准方程为 +
+ =1,a>b>0,
=1,a>b>0,
∴a2=b2+4,即椭圆的方程为 +
+ =1.
=1.
∵点(-2,- )在椭圆上,
)在椭圆上,
∴ +
+ =1.
=1.
解得b2=4或b2=-2(舍).
由此得a2=8,即椭圆的标准方程为 +
+ =1.
=1.
(2)证明:设直线l的方程为y=kx+m,
与椭圆C的交点A(x1,y1)、B(x2,y2),
y=kx+m,
则有 +
+ =1.
=1.
解得(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0.
∵△>0,∴m2<b2+a2k2,
即- <m<
<m< .
.
则x1+x2=- ,y1+y2=kx1+m+kx2+m=
,y1+y2=kx1+m+kx2+m= ,
,
∴AB中点M的坐标为(- ,
, ).
).
∴线段AB的中点M在过原点的直线b2x+a2ky=0上.
(3)解:如图,作两条平行直线分别交椭圆于A、B和C、D,并分别取AB、CD的中点M、N,连接直线MN;又作两条平行直线(与前两条直线不平行)分别交椭圆于A1、B1和C1、D1,并分别取A1B1、C1D1的中点M1、N1,连接直线M1N1,那么直线MN和M1N1的交点O即为椭圆中心.
点评:本题主要考查了椭圆的标准方程和椭圆与直线的关系.综合考查了学生对椭圆性质和利用韦达定理来解决椭圆与直线问题的掌握.
 )代入椭圆方程,求得b,进而根据a=
)代入椭圆方程,求得b,进而根据a= 求得a,椭圆的方程可得.
求得a,椭圆的方程可得.(2)设直线l的方程为y=kx+m且椭圆C的交点A(x1,y1)、B(x2,y2),直线方程和椭圆方程联立进而可得x1+x2和y1+y2的表达式,进而可得AB中点M的坐标进而可判定AB的中点M在过原点的直线b2x+a2ky=0上.
(3)作两条平行直线分别交椭圆于A、B和C、D,并分别取AB、CD的中点M、N,连接直线MN;又作两条平行直线(与前两条直线不平行)分别交椭圆于A1、B1和C1、D1,并分别取A1B1、C1D1的中点M1、N1,连接直线M1N1,那么直线MN和M1N1的交点O即为椭圆中心.
解答:
 解:(1)设椭圆的标准方程为
解:(1)设椭圆的标准方程为 +
+ =1,a>b>0,
=1,a>b>0,∴a2=b2+4,即椭圆的方程为
 +
+ =1.
=1.∵点(-2,-
 )在椭圆上,
)在椭圆上,∴
 +
+ =1.
=1.解得b2=4或b2=-2(舍).
由此得a2=8,即椭圆的标准方程为
 +
+ =1.
=1.(2)证明:设直线l的方程为y=kx+m,
与椭圆C的交点A(x1,y1)、B(x2,y2),
y=kx+m,
则有
 +
+ =1.
=1.解得(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0.
∵△>0,∴m2<b2+a2k2,
即-
 <m<
<m< .
.则x1+x2=-
 ,y1+y2=kx1+m+kx2+m=
,y1+y2=kx1+m+kx2+m= ,
,∴AB中点M的坐标为(-
 ,
, ).
).∴线段AB的中点M在过原点的直线b2x+a2ky=0上.
(3)解:如图,作两条平行直线分别交椭圆于A、B和C、D,并分别取AB、CD的中点M、N,连接直线MN;又作两条平行直线(与前两条直线不平行)分别交椭圆于A1、B1和C1、D1,并分别取A1B1、C1D1的中点M1、N1,连接直线M1N1,那么直线MN和M1N1的交点O即为椭圆中心.
点评:本题主要考查了椭圆的标准方程和椭圆与直线的关系.综合考查了学生对椭圆性质和利用韦达定理来解决椭圆与直线问题的掌握.

练习册系列答案
相关题目
 (1)求右焦点坐标是(2,0),且经过点(-2,-
(1)求右焦点坐标是(2,0),且经过点(-2,- 的椭圆的标准方程;
的椭圆的标准方程; 有共同的焦点并且与双曲线
有共同的焦点并且与双曲线 有共同渐近线的双曲线方程.
有共同渐近线的双曲线方程.