题目内容

14、设f（x）定义在R上的奇函数，且f（x+3）=-f（x），则f（2010）=

0

．

分析：由题意可得函数是奇函数所以f（0）=0，结合题意（x+3）=-f（x）可得，函数是周期函数且周期为6，进而得到答案．

解答：解：因为f（x）定义在R上的奇函数，
所以f（-x）=-f（x），所以f（0）=0．
又因为f（x+3）=-f（x），
所以f（x+6）=f[（x+3）+3]=-f（x+3）=f（x）．
即f（x+6）=f（x）．
所以f（x）是周期函数，且周期为6．
所以f（2010）=f（0）=0．
故答案为：0．．

点评：解决此类问题的关键是熟练掌握函数的性质，如奇偶性、单调性、周期性等性质．

练习册系列答案

点睛新教材全能解读系列答案

快乐成长小考总复习系列答案

小考神童系列答案

小学教材完全解读系列答案

英语听力模拟题系列答案

优翼阅读给力系列答案

领航中考命题调研系列答案

初中古诗文详解系列答案

口算应用题卡系列答案

中考考点经典新题系列答案

相关题目

设f（x）定义在R上的偶函数，且f(x+3)=-

，又当x∈（0，3]时，f（x）=2x，则f（2007）=

设f（x）定义在R₊上，对于任意a、b∈R₊，有f（ab）=f（a）+f（b）求证：
（1）f（1）=0；
（2）f（

）=-f（x）；
（3）若x∈（1，+∞）时，f（x）＜0，则f（x）在（1，+∞）上是减函数．

设f（x）定义在R₊上，对于任意a、b∈R₊，有f（ab）=f（a）+f（b）求证：
（1）f（1）=0；
（2）f（ $数学公式$ ）=-f（x）；
（3）若x∈（1，+∞）时，f（x）＜0，则f（x）在（1，+∞）上是减函数．

设f（x）定义在R上的偶函数，且

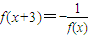，又当x∈（0，3]时，f（x）=2x，则f（2007）= ．