题目内容
已知全集U={x|x≤4},集合A={x|-2<x<3},集合B={x|-3≤x≤2}.求A∩B,(?UA)∪B,A∩(?UB),(?UA)∪(?UB).
分析:根据交集、补集、并集的定义以及借助数轴解答即可.
解答:解:如下图所示,在数轴上表示全集U及集合A,B.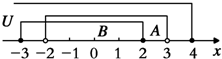
∵A={x|-2<x<3},
B={x|-3≤x≤3}.
∴?UA={x|x≤-2,或3≤x≤4},
?UB={x|x<-3,或2<x≤4}.
∴A∩B={x|-2<x≤2};
(?UA)∪B={x|x≤2,或3≤x≤4};
A∩(?UB)={x|2<x<3};
(?UA)∪(?UB)={x|x≤-2,或2<x≤4}.

∵A={x|-2<x<3},
B={x|-3≤x≤3}.
∴?UA={x|x≤-2,或3≤x≤4},
?UB={x|x<-3,或2<x≤4}.
∴A∩B={x|-2<x≤2};
(?UA)∪B={x|x≤2,或3≤x≤4};
A∩(?UB)={x|2<x<3};
(?UA)∪(?UB)={x|x≤-2,或2<x≤4}.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目