题目内容

解答下列问题：
（I）设f(x)=
x2-9
(x≤-3)，
（1）求f（x）的反函数f-1（x）；
（2）若u1=1，un=-f-1(un-1)，(n≥2)，求un；
（3）若ak=
1
uk+uk+1
，k=1，2，3，…，求数列{an}的前n项和Sn．
（1）由y=f(x)=
x2-9
(x≤-3)，两边平方得出y2=x2-9，移向得，x2=y2+9
∵x≤-3，∴两边开方得出x=-
y2+9
，（y≥0）
所以反函数为y=f-1(x)=-
x2+9
（x≥0）
（2）由un=-f-1(un-1)得出un=-f-1(un-1)=
un-12+9
（n≥2），两边平方并移向得出un2-un-12=9
所以数列{un2}是公差为9的等差数列，且首项u12=1，
un2=1+（n-1）×9=9n-8，
∵un＞0，∴un=
9n-8

（3）ak=
1
9k-8
+
9k+1
=
1
9
(
9k+1
-
9k-8
)，
∴Sn=
1
9
[(
10
-1)+(
19
-
10
)+…+(
9n+1
-
9n-8
)]
=
1
9
(
9n+1
-1)；
练习册系列答案
相关题目
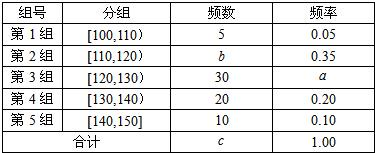精英家教网某校通过数学竞赛，选出成绩不低于100分的学生成绩进行统计（得分均为整数，满分150分），得频率分布表：
请根据频率分布表中所提供的数据，解答下列问题：
（I）求a、b、c的值及随机抽取一考生其成绩不低于120分的概率；
（II）若从成绩不低于120分的3、4、5组中按分层抽样的方法抽取6人参加数学实践活动，并在这6人中指定2名负责人，求从第4组抽取的学生中至少有一名是负责人的概率．
（2012•福建）受轿车在保修期内维修费等因素的影响，企业产生每辆轿车的利润与该轿车首次出现故障的时间有关，某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年，现从该厂已售出的两种品牌轿车中随机抽取50辆，统计数据如下：
品牌          甲       乙
首次出现故障时间x（年） 0＜x＜1 1＜x≤2 x＞2 0＜x≤2 x＞2
轿车数量（辆） 2 3 45 5 45
每辆利润（万元） 1 2 3 1.8 2.9
将频率视为概率，解答下列问题：
（I）从该厂生产的甲品牌轿车中随机抽取一辆，求首次出现故障发生在保修期内的概率；
（II）若该厂生产的轿车均能售出，记住生产一辆甲品牌轿车的利润为X1，生产一辆乙品牌轿车的利润为X2，分别求X1，X2的分布列；
（III）该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌轿车，若从经济效益的角度考虑，你认为应该产生哪种品牌的轿车？说明理由．
（2013•成都二模）某校高三（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，可见部分如下：

试根据图表中的信息解答下列问题：
（I）求全班的学生人数及分数在[70，80）之间的频数；
（II）为快速了解学生的答题情况，老师按分层抽样的方法从位于[70，80），[80，90）和[90，100]分数段的试卷中抽取8份进行分析，再从中任选3人进行交流，求交流的学生中，成绩位于[70，80）分数段的人数X的分布列和数学期望．
解答下列问题：
（I）设f(x)=
x2-9
(x≤-3)，
（1）求f（x）的反函数f-1（x）；
（2）若u1=1，un=-f-1(un-1)，(n≥2)，求un；
（3）若ak=
1
uk+uk+1
，k=1，2，3，…，求数列{an}的前n项和Sn．

（ 14 分） 受轿车在保修期内维修费等因素的影响， 企业产生每辆轿车的利润与该轿车首次出现故障的时间有关，某轿车制造厂生产甲、乙两种品牌轿车，保修期均为 2 年，现从该厂已售出的两 种品牌轿车中随机抽取 50 辆，统计数据如下：

将频率视为概率，解答下列问题：

（I）从该厂生产的甲品牌轿车中随机抽取一辆，求首次出现故障发生在保修期内的概率；

(II)若该厂生产的轿车均能售出，记住生产一辆甲品牌轿车的利润为 ，生产一辆乙品牌轿 车的利润为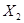 ，分别求 ， 的分布列 ；

（III）该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一 种品牌轿 车，若从经济效益的角度考虑，你认为应该产生哪种品牌的轿车？说明理由.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网