题目内容
例1:试判断以下各组函数是否表示同一函数?
(1)f(x)=
,g(x)=
;
(2)f(x)=
,g(x)=
(3)f(x)=
,g(x)=(
)2n-1(n∈N*);
(4)f(x)=
,g(x)=
;
(5)f(x)=x2-2x-1,g(t)=t2-2t-1.
(1)f(x)=
| x2 |
| 3 | x3 |
(2)f(x)=
| |x| |
| x |
|
(3)f(x)=
| 2n+1 | x2n+1 |
| 2n-1 | x |
(4)f(x)=
| x |
| x+1 |
| x2+x |
(5)f(x)=x2-2x-1,g(t)=t2-2t-1.
(1)由于f(x)=
=|x|,g(x)=
=x,故它们的值域及对应法则都不相同,所以它们不是同一函数.
(2)由于函数f(x)=
的定义域为(-∞,0)∪(0,+∞),而g(x)=
的定义域为R,所以它们不是同一函数.
(3)由于当n∈N*时,2n±1为奇数,∴f(x)=
=x,g(x)=(
)2n-1=x,它们的定义域、值域及对应法则都相同,所以它们是同一函数.
(4)由于函数f(x)=
的定义域为{x|x≥0},而g(x)=
的定义域为{x|x≤-1或x≥0},它们的定义域不同,所以它们不是同一函数.
(5)函数的定义域、值域和对应法则都相同,所以它们是同一函数.
故(3)(5)都表示同一函数.
| x2 |
| 3 | x3 |
(2)由于函数f(x)=
| |x| |
| x |
|
(3)由于当n∈N*时,2n±1为奇数,∴f(x)=
| 2n+1 | x2n+1 |
| 2n-1 | x |
(4)由于函数f(x)=
| x |
| x+1 |
| x2+x |
(5)函数的定义域、值域和对应法则都相同,所以它们是同一函数.
故(3)(5)都表示同一函数.

练习册系列答案
相关题目
 ,g(x)=
,g(x)=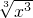 ;
;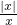 ,g(x)=
,g(x)=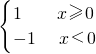
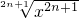 ,g(x)=(
,g(x)=(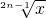 )2n-1(n∈N*);
)2n-1(n∈N*);
 ,g(x)=
,g(x)=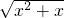 ;
; ,g(x)=
,g(x)= ;
;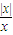 ,g(x)=
,g(x)=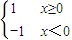
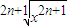 ,g(x)=(
,g(x)=(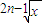 )2n-1(n∈N*);
)2n-1(n∈N*);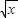
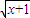 ,g(x)=
,g(x)=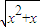 ;
;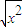 ,g(x)=
,g(x)=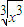 ;
;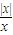 ,g(x)=
,g(x)=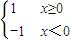
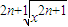 ,g(x)=(
,g(x)=(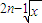 )2n-1(n∈N*);
)2n-1(n∈N*);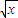
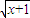 ,g(x)=
,g(x)=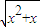 ;
;