题目内容
例1:试判断以下各组函数是否表示同一函数?(1)f(x)=
| x2 |
| 3 | x3 |
(2)f(x)=
| |x| |
| x |
|
(3)f(x)=
| 2n+1 | x2n+1 |
| 2n-1 | x |
(4)f(x)=
| x |
| x+1 |
| x2+x |
(5)f(x)=x2-2x-1,g(t)=t2-2t-1.
分析:对于两个函数y=f(x)和y=g(x),当且仅当它们的定义域、值域、对应法则都相同时,y=f(x)和y=g(x)才表示同一函数.若两个函数表示同一函数,则它们的图象完全相同,反之亦然.
解答:解:(1)由于f(x)=
=|x|,g(x)=
=x,故它们的值域及对应法则都不相同,所以它们不是同一函数.
(2)由于函数f(x)=
的定义域为(-∞,0)∪(0,+∞),而g(x)=
的定义域为R,所以它们不是同一函数.
(3)由于当n∈N*时,2n±1为奇数,∴f(x)=
=x,g(x)=(
)2n-1=x,它们的定义域、值域及对应法则都相同,所以它们是同一函数.
(4)由于函数f(x)=
的定义域为{x|x≥0},而g(x)=
的定义域为{x|x≤-1或x≥0},它们的定义域不同,所以它们不是同一函数.
(5)函数的定义域、值域和对应法则都相同,所以它们是同一函数.
故(3)(5)都表示同一函数.
| x2 |
| 3 | x3 |
(2)由于函数f(x)=
| |x| |
| x |
|
(3)由于当n∈N*时,2n±1为奇数,∴f(x)=
| 2n+1 | x2n+1 |
| 2n-1 | x |
(4)由于函数f(x)=
| x |
| x+1 |
| x2+x |
(5)函数的定义域、值域和对应法则都相同,所以它们是同一函数.
故(3)(5)都表示同一函数.
点评:(1)第(5)小题易错判断成它们是不同的函数,原因是对函数的概念理解不透.要知道,在函数的定义域及对应法则f不变的条件下,自变量变换字母,以至变换成其他字母的表达式,这对于函数本身并无影响,比如f(x)=x2+1,f(t)=t2+1,f(u+1)=(u+1)2+1都可视为同一函数.
(2)对于两个函数来讲,只要函数的三要素中有一要素不相同,则这两个函数就不可能是同一函数.
(2)对于两个函数来讲,只要函数的三要素中有一要素不相同,则这两个函数就不可能是同一函数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,g(x)=
,g(x)=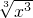 ;
;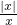 ,g(x)=
,g(x)=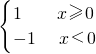
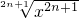 ,g(x)=(
,g(x)=(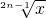 )2n-1(n∈N*);
)2n-1(n∈N*);
 ,g(x)=
,g(x)=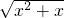 ;
; ,g(x)=
,g(x)= ;
;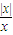 ,g(x)=
,g(x)=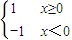
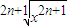 ,g(x)=(
,g(x)=(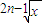 )2n-1(n∈N*);
)2n-1(n∈N*);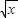
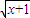 ,g(x)=
,g(x)=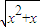 ;
;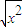 ,g(x)=
,g(x)=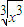 ;
;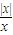 ,g(x)=
,g(x)=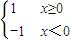
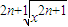 ,g(x)=(
,g(x)=(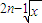 )2n-1(n∈N*);
)2n-1(n∈N*);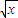
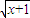 ,g(x)=
,g(x)=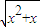 ;
;