题目内容
 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心(1)求证:PQ∥平面BCC1B1
(2)求PQ与面A1B1BA所成的角.
分析:(1)连接AB1,B1C,由△AB1C中,P、Q分别是AB1、AC的中点知PQ∥B1C,由此能够证明PQ∥平面BCC1B1.
(2)由PQ∥B1C,知PQ与面A1B1BA所成的角即为B1C与面A1B1BA所成的角,由正方体中BC与面A1B1BA垂直,知∠BB1C即为B1C与面A1B1BA所成的角,由此能求出PQ与面A1B1BA所成的角.
(2)由PQ∥B1C,知PQ与面A1B1BA所成的角即为B1C与面A1B1BA所成的角,由正方体中BC与面A1B1BA垂直,知∠BB1C即为B1C与面A1B1BA所成的角,由此能求出PQ与面A1B1BA所成的角.
解答:(本小题满分8分)
(1)证明:连接AB1,B1C,
∵△AB1C中,P、Q分别是AB1、AC的中点,∴PQ∥B1C,…2分
又PQ在平面BCC1B1外面,B1C?平面BCC1B1,
∴PQ∥平面BCC1B1.…4分
(2)解:由(1)知PQ∥B1C,
所以PQ与面A1B1BA所成的角即为B1C与面A1B1BA所成的角,…6分
正方体中BC与面A1B1BA垂直,
所以∠BB1C即为B1C与面A1B1BA所成的角,…7分
∵∠BB1C=
,所以PQ与面A1B1BA所成的角
.…8分
(1)证明:连接AB1,B1C,
∵△AB1C中,P、Q分别是AB1、AC的中点,∴PQ∥B1C,…2分
又PQ在平面BCC1B1外面,B1C?平面BCC1B1,
∴PQ∥平面BCC1B1.…4分
(2)解:由(1)知PQ∥B1C,
所以PQ与面A1B1BA所成的角即为B1C与面A1B1BA所成的角,…6分
正方体中BC与面A1B1BA垂直,
所以∠BB1C即为B1C与面A1B1BA所成的角,…7分
∵∠BB1C=
| π |
| 4 |
| π |
| 4 |
点评:本题考查直线与平面平等的证明,考查直线与平面所成角的求法,解题时要认真审题,恰当地进行等价转化,能够化空间问题为平面问题.

练习册系列答案
相关题目
 如图所示,已知P,Q分别是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心,证明:PQ∥平面BCC1B1.
如图所示,已知P,Q分别是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心,证明:PQ∥平面BCC1B1.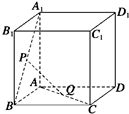
 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心