题目内容
 如图所示,已知P,Q分别是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心,证明:PQ∥平面BCC1B1.
如图所示,已知P,Q分别是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心,证明:PQ∥平面BCC1B1.分析:连接AB1、AC、B1C,由题意可得故PQ是△AB1C的中位线,故有PQ平行且等于
B1C.再根据直线和平面平行的判定定理证得PQ∥平面BCC1B1.
| 1 |
| 2 |
解答: 证明:连接AB1、AC、B1C,由于P,Q分别是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心,
证明:连接AB1、AC、B1C,由于P,Q分别是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心,
故PQ是△AB1C的中位线,故有PQ平行且等于
B1C.
而B1C?平面BCC1B1,而 PQ不在平面 BCC1B1内,故有PQ∥平面BCC1B1.
 证明:连接AB1、AC、B1C,由于P,Q分别是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心,
证明:连接AB1、AC、B1C,由于P,Q分别是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心,故PQ是△AB1C的中位线,故有PQ平行且等于
| 1 |
| 2 |
而B1C?平面BCC1B1,而 PQ不在平面 BCC1B1内,故有PQ∥平面BCC1B1.
点评:本题主要考查三角形的中位线的性质,直线和平面平行的判定定理的应用,属于中档题.

练习册系列答案
相关题目
 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心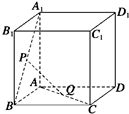
 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD中心