Question

已知f（x）=

x ，x≥0 e-x-ex，x＜0

若函数y=f（x）-k（x+1）有三个零点，则实数k的取值范围是（　　）

• A．（-

  1

  2

  ，0）
• B．（0，

  1

  2

  ）
• C．（

  1

  2

  ，1）
• D．（1，+∞）

Answer 1

分析：由y=f（x）-k（x+1）=0得f（x）=k（x+1），设y=f（x），y=k（x+1），然后作出图象，利用数形结合的思想确定实数k的取值范围．

解答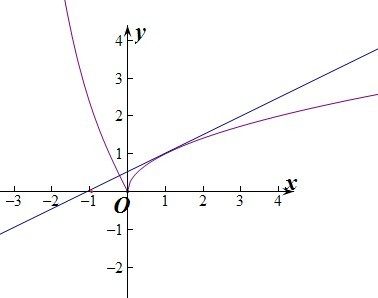：解：y=f（x）-k（x+1）=0得f（x）=k（x+1），
设y=f（x），y=k（x+1），在同一坐标系中作出函数y=f（x）和y=k（x+1）的图象如图：
因为当x＜0时，函数f（x）=e^-x-e^x单调递减，且f（x）＞0．
由图象可以当直线y=k（x+1）与f(x)=

x

相切时，函数y=f（x）-k（x+1）
有两个零点．下面求切线的斜率．由

y=k(x+1) y= x

得k²x²+（2k²-1）x+k²=0，
当k=0时，不成立．
由△=0得△=（2k²-1）²-4k²?k²=1-4k²=0，解得k2=

1

4

，
所以k=

1

2

或k=-

1

2

（不合题意舍去）．
所以要使函数y=f（x）-k（x+1）有三个零点，
则0＜k＜

1

2

．
故选B．

点评：本题综合考查了函数的零点问题，利用数形结合的思想是解决本题的关键．综合性较强，难度较大．