题目内容
已知椭圆C的中心在坐标原点,焦点在x轴上,离心率 ,且点P(-2,0)在椭圆C上.
,且点P(-2,0)在椭圆C上.(Ⅰ)求椭圆C的方程;
(Ⅱ)已知A、B为椭圆C上的动点,当PA⊥PB时,求证:直线AB恒过一个定点.并求出该定点的坐标.
【答案】分析:(1)设椭圆的方程为: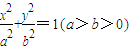 ,由题意得
,由题意得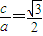 ,a=2,再由b2=a2-c2可求得c,b;
,a=2,再由b2=a2-c2可求得c,b;
(2)分情况讨论:①当直线l不垂直于x轴时,设AB:y=kx+m,A(x1,y1)B(x2,y2),与椭圆方程联立方程组消掉y得x的一元二次方程,由韦达定理即及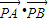 =0可得m,k的关系式,分别代入直线方程可求得定点坐标,②当直线l垂直于x轴时,直线AB:
=0可得m,k的关系式,分别代入直线方程可求得定点坐标,②当直线l垂直于x轴时,直线AB: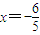 ,检验即可;
,检验即可;
解答:解:(1)设椭圆的方程为: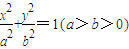 ,
,
由题意得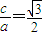 ,a=2,所以c=
,a=2,所以c=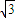 ,
,
又b2=a2-c2=1,
所以椭圆的方程为: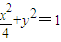 ;
;
(2)①当直线l不垂直于x轴时,设AB:y=kx+m,A(x1,y1)B(x2,y2),
由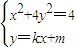 ,得(1+4k2)x2+8kmx+4(m2-1)=0,
,得(1+4k2)x2+8kmx+4(m2-1)=0,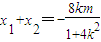 ,
, ,
,
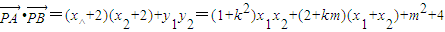 =
=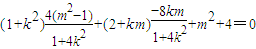 ,
,
∴12k2+5m2-16km=0,即(6k-5m)(2k-m)=0,解得 ,
,
当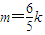 时,
时,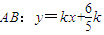 恒过定点
恒过定点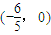 ;
;
当m=2k时,AB:y=kx+2k恒过定点(-2,0),不符合题意舍去;
②当直线l垂直于x轴时,直线AB: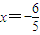 ,则AB与椭圆C相交于
,则AB与椭圆C相交于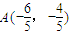 ,
,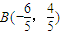 ,
,
∴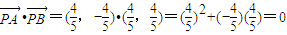 ,∵PA⊥PB,满足题意,
,∵PA⊥PB,满足题意,
综上可知,直线AB恒过定点,且定点坐标为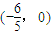 .
.
点评:本题考查直线与圆锥曲线的位置关系及椭圆方程的求解,考查分类讨论思想,考查学生分析问题解决问题的能力.
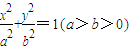 ,由题意得
,由题意得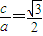 ,a=2,再由b2=a2-c2可求得c,b;
,a=2,再由b2=a2-c2可求得c,b;(2)分情况讨论:①当直线l不垂直于x轴时,设AB:y=kx+m,A(x1,y1)B(x2,y2),与椭圆方程联立方程组消掉y得x的一元二次方程,由韦达定理即及
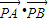 =0可得m,k的关系式,分别代入直线方程可求得定点坐标,②当直线l垂直于x轴时,直线AB:
=0可得m,k的关系式,分别代入直线方程可求得定点坐标,②当直线l垂直于x轴时,直线AB: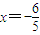 ,检验即可;
,检验即可;解答:解:(1)设椭圆的方程为:
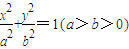 ,
,由题意得
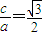 ,a=2,所以c=
,a=2,所以c=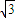 ,
,又b2=a2-c2=1,
所以椭圆的方程为:
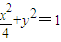 ;
;(2)①当直线l不垂直于x轴时,设AB:y=kx+m,A(x1,y1)B(x2,y2),
由
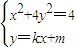 ,得(1+4k2)x2+8kmx+4(m2-1)=0,
,得(1+4k2)x2+8kmx+4(m2-1)=0,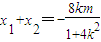 ,
, ,
,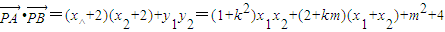 =
=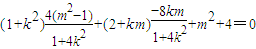 ,
,∴12k2+5m2-16km=0,即(6k-5m)(2k-m)=0,解得
 ,
,当
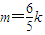 时,
时,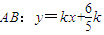 恒过定点
恒过定点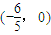 ;
;当m=2k时,AB:y=kx+2k恒过定点(-2,0),不符合题意舍去;
②当直线l垂直于x轴时,直线AB:
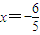 ,则AB与椭圆C相交于
,则AB与椭圆C相交于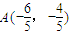 ,
,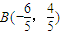 ,
,∴
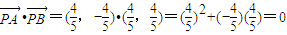 ,∵PA⊥PB,满足题意,
,∵PA⊥PB,满足题意,综上可知,直线AB恒过定点,且定点坐标为
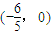 .
.点评:本题考查直线与圆锥曲线的位置关系及椭圆方程的求解,考查分类讨论思想,考查学生分析问题解决问题的能力.

练习册系列答案
相关题目
 已知椭圆C的中心在坐标原点,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点P(1,
已知椭圆C的中心在坐标原点,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点P(1,