题目内容
 已知椭圆C的中心在坐标原点,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点P(1,
已知椭圆C的中心在坐标原点,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点P(1,| 3 | 2 |
(I)求椭圆C的方程;
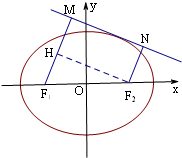
(II)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2M⊥l,求四边形F1MNF2面积S的最大值.
分析:(Ⅰ)由题意设出椭圆的标准方程,题目给出c=1,把点P的坐标带入椭圆方程,结合a2=b2+c2求解a,b的值,则椭圆的方程可求;
(Ⅱ)联立直线方程和椭圆方程,由判别式等于0得到直线的斜率和截距的关系,由点到直线距离公式分别求出F1,F2 到直线的距离,把距离作差后结合直线的倾斜角把
|MN|用距离差的绝对值和直线的斜率表示,然后代入直角梯形的面积公式,转化为含有一个变量的代数式后换元,最后利用导数求最值.
(Ⅱ)联立直线方程和椭圆方程,由判别式等于0得到直线的斜率和截距的关系,由点到直线距离公式分别求出F1,F2 到直线的距离,把距离作差后结合直线的倾斜角把
|MN|用距离差的绝对值和直线的斜率表示,然后代入直角梯形的面积公式,转化为含有一个变量的代数式后换元,最后利用导数求最值.
解答:解:(I)设椭圆C的方程为
+
=1 (a>b>0),
由已知可得
,
解得:a=2,b=
,
故所求椭圆方程为
+
=1;
(II)如图,
 由
由
,得(4k2+3)x2+8kmx+4m2-12=0.
由直线l与椭圆C仅有一个公共点知,
△=64k2m2-4(4k2+3)(4m2-12)=0,化简得:m2=4k2+3.
设d1=|F1M|=
,d2=|F2M|=
.
当k≠0时,设直线l的倾斜角为θ,则|d1-d2|=|MN||tanθ|,
∴|MN|=|
|,
S=
|
|(d1+d2)=|
|
=
=
=
.
∵m2=4k2+3,∴当k≠0时,|m|=
,令g(t)=t+
,t=|m|>
,g′(t)=1-
,
当t>
时,g′(t)>0,∴g(t)在[
,+∞)上为增函数,
∴g(t)>g(
)=
,∴S<2
.
当k=0时,四边形F1MNF2是矩形,S=2
.
所以四边形F1MNF2面积S的最大值为2
.
| x2 |
| a2 |
| y2 |
| b2 |
由已知可得
|
解得:a=2,b=
| 3 |
故所求椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)如图,
 由
由
|
由直线l与椭圆C仅有一个公共点知,
△=64k2m2-4(4k2+3)(4m2-12)=0,化简得:m2=4k2+3.
设d1=|F1M|=
| |-k+m| | ||
|
| |k+m| | ||
|
当k≠0时,设直线l的倾斜角为θ,则|d1-d2|=|MN||tanθ|,
∴|MN|=|
| d1-d2 |
| k |
S=
| 1 |
| 2 |
| d1-d2 |
| k |
| d12-d22 |
| 2k |
=
| 2|m| |
| k2+1 |
| 2|m| | ||
|
| 8 | ||
|m|+
|
∵m2=4k2+3,∴当k≠0时,|m|=
| 3 |
| 1 |
| t |
| 3 |
| 1 |
| t2 |
当t>
| 3 |
| 3 |
∴g(t)>g(
| 3 |
4
| ||
| 3 |
| 3 |
当k=0时,四边形F1MNF2是矩形,S=2
| 3 |
所以四边形F1MNF2面积S的最大值为2
| 3 |
点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的关系,考查了数学转化思想方法,训练了利用函数的导函数求最值,考查了学生灵活处理问题的能力和计算能力,是高考试题中的压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目