题目内容
7.已知函数 f(x)=alnx-x+1,g(x)=-x2+(a+1)x+1.(1)若对任意的 x∈[1,e],不等式 f(x)≥g(x)恒成立,求实数a的取值范围;
(2)若函数 h(x)在其定义城内存在实数 x0,使得 h(x0+k)=h(x0)+h(k)(k≠0且为常数)成立,则称函数h(x)为保k阶函数,已知 H(x)=f(x)-(a-1)x+a-1为保a阶函数,求实数a的取值范围.
分析 (1)把对任意的 x∈[1,e],不等式 f(x)≥g(x)恒成立,转化为a(x-lnx)≤x2-2x恒成立,再由x-lnx>0得$a≤\frac{{x}^{2}-2x}{x-lnx}$恒成立.构造函数F(x)=$\frac{{x}^{2}-2x}{x-lnx}$,利用导数求其最小值得答案;
(2)由H(x)=f(x)-(a-1)x+a-1=alnx-x+1-ax+x+a-1=alnx-ax+a(x>0),根据保a阶函数的概念列式,整理得到ln(x0+a)-(x0+a)+1=lnx0-x0+1+lna-a+1,即ln(x0+a)=lnx0+lna+1,转化为$a=\frac{1}{e-\frac{1}{{x}_{0}}}$,由x0>0可得实数a的取值范围是$a>\frac{1}{e}$.
解答 解:(1)∵对任意的 x∈[1,e],不等式 f(x)≥g(x)恒成立,
即alnx-x+1≥-x2+(a+1)x+1恒成立,a(x-lnx)≤x2-2x恒成立,
∵x∈[1,e],∴lnx≤lne=1≤x,
∵上式等号不能同时成立,∴lnx<x,
即x-lnx>0,∴$a≤\frac{{x}^{2}-2x}{x-lnx}$恒成立.
令F(x)=$\frac{{x}^{2}-2x}{x-lnx}$,∴a≤F(x)min(x∈[1,e]),
由于${F}^{′}(x)=\frac{(x-1)(x+2-2lnx)}{(x-lnx)^{2}}$,
由于1≤x≤e,∴x-1>0,x+2-2lnx=x+2(1-lnx)>0,
∴F′(x)>0.
∴函数F(x)=$\frac{{x}^{2}-2x}{x-lnx}$在区间[1,e]上单调递增,
∴F(x)≥F(1)=$\frac{{1}^{2}-2}{1-ln1}=-1$.
∴a≤-1;
(2)∵H(x)=f(x)-(a-1)x+a-1=alnx-x+1-ax+x+a-1=alnx-ax+a(x>0),
根据保a阶函数的概念,∴存在x0>0,使得H(x0+a)=H(x0)+H(a),
即a[ln(x0+a)-(x0+a)+1]=a(lnx0-x0+1)+a(lna-a+1)=a(lnx0-x0+1+lna-a+1),
∴ln(x0+a)-(x0+a)+1=lnx0-x0+1+lna-a+1,
即ln(x0+a)=lnx0+lna+1,
即$ln(\frac{{x}_{0}+a}{a{x}_{0}})=1$,∴$\frac{{x}_{0}+a}{a{x}_{0}}=e$.
∴$a=\frac{1}{e-\frac{1}{{x}_{0}}}$,
∵x0>0,∴a$>\frac{1}{e}$.
∴实数a的取值范围是$a>\frac{1}{e}$.
点评 本题考查了利用导数研究函数的单调性,考查了利用导数求函数的最值,考查了数学转化与化归、分离参数等数学思想方法,着重考查恒成立问题的解法,难度较大.

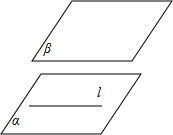
| A. | α∩β=l | B. | α∥β,l∈α | C. | l∥β,l?α | D. | α∥β,l?α |
 已知椭圆C:$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<$\sqrt{2}$),斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,向量$\overrightarrow{OA}$+$\overrightarrow{OB}$与向量$\overrightarrow{a}$=(2,-1)共线.
已知椭圆C:$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<$\sqrt{2}$),斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,向量$\overrightarrow{OA}$+$\overrightarrow{OB}$与向量$\overrightarrow{a}$=(2,-1)共线.