题目内容
若AB=2, AC=
![]() 解析:本小题考查三角形面积公式、余弦定理以及函数思想.设BC=x,则AC=
解析:本小题考查三角形面积公式、余弦定理以及函数思想.设BC=x,则AC=![]() x,
x,
根据面积公式得S△ABC=![]() AB·BCsinB=
AB·BCsinB=![]() ×2x
×2x![]() ,
,
根据余弦定理得cosB=![]()
=![]() ,
,
代入上式得S△ABC=x![]() ,
,
由三角形三边关系有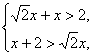
解得2![]() -2<x<2
-2<x<2![]() +2.
+2.
故当x=2![]() 时S△ABC取得最大值2
时S△ABC取得最大值2![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
题目内容
若AB=2, AC=
![]() 解析:本小题考查三角形面积公式、余弦定理以及函数思想.设BC=x,则AC=
解析:本小题考查三角形面积公式、余弦定理以及函数思想.设BC=x,则AC=![]() x,
x,
根据面积公式得S△ABC=![]() AB·BCsinB=
AB·BCsinB=![]() ×2x
×2x![]() ,
,
根据余弦定理得cosB=![]()
=![]() ,
,
代入上式得S△ABC=x![]() ,
,
由三角形三边关系有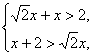
解得2![]() -2<x<2
-2<x<2![]() +2.
+2.
故当x=2![]() 时S△ABC取得最大值2
时S△ABC取得最大值2![]() .
.

 优等生题库系列答案
优等生题库系列答案