题目内容
平面内有两个顶点F1，F2和一动点M，设命题甲：||MF1|-|MF2||是定值；命题乙：点M的轨迹是双曲线．则命题甲是命题乙的
必要不充分
必要不充分
条件．分析：根据双曲线的定义，利用充分条件和必要条件的定义进行判断．
解答：解：若点M的轨迹是双曲线，则根据双曲线的定义可知||MF1|-|MF2||是定值．
若||MF1|-|MF2||是定值，当定值等于F1F2时，则点M的轨迹不是双曲线，
∴命题甲是命题乙的必要不充分条件．
故答案为：必要不充分
若||MF1|-|MF2||是定值，当定值等于F1F2时，则点M的轨迹不是双曲线，
∴命题甲是命题乙的必要不充分条件．
故答案为：必要不充分
点评：本题主要考查充分条件和必要条件的判断，利用双曲线的定义是解决本题的关键．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
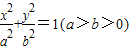的两个焦点为F1，F2，椭圆的离心率为
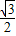，P点是椭圆上任意一点，且|PF1|+|PF2|=4，
的两个焦点为F1，F2，椭圆的离心率为
，P点是椭圆上任意一点，且|PF1|+|PF2|=4，