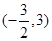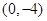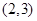题目内容
曲线 上的点到直线
上的点到直线 的最短距离是( )
的最短距离是( )
A. | B. | C. | D.0 |
B
解析试题分析:∵曲线y=ln(2x-1),
∴y′=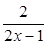 ,分析知直线2x-y+8=0与曲线y=ln(2x-1)相切的点到直线2x-y+8=0的距离最短,
,分析知直线2x-y+8=0与曲线y=ln(2x-1)相切的点到直线2x-y+8=0的距离最短,
y′═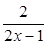 =2,解得x=1,把x=1代入y=ln(2x-1),
=2,解得x=1,把x=1代入y=ln(2x-1),
∴y=0,∴点(1,0)到直线2x-y+8=0的距离最短,
∴d=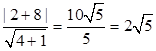 ,
,
故答案为B..
考点:利用导数研究曲线上某点切线方程;两条平行直线间的距离..

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
函数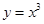 与
与 轴,直线
轴,直线 围成的封闭图形的面积为( )
围成的封闭图形的面积为( )
A.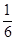 | B.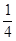 | C. | D. |
已知点P(1,2)是曲线y=2x2上一点,则P处的瞬时变化率为 ( )
| A.2 | B.4 | C.6 | D.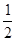 |
曲线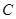 :
: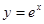 在点
在点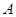 处的切线
处的切线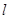 恰好经过坐标原点,则曲线
恰好经过坐标原点,则曲线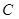 直线
直线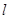 ,
,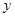 轴围成的图形面积为( )
轴围成的图形面积为( )
A. | B.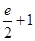 | C.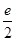 | D.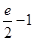 |
曲线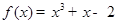 在
在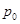 处的切线平行于直线
处的切线平行于直线 ,则
,则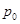 点的坐标为( )
点的坐标为( )
A.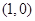 | B.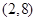 |
C.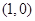 和 和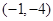 | D.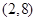 和 和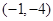 |
函数 的最大值是( )
的最大值是( )
A.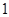 | B.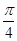 | C.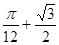 | D.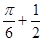 |
若曲线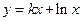 在点
在点 处的切线平行于x轴,则k= ( )
处的切线平行于x轴,则k= ( )
| A.-1 |
| B.1 |
| C.-2 |
| D.2 |
设函数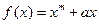 的导数
的导数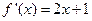 ,则数列
,则数列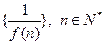 的前n项和( )
的前n项和( )
A. |
B.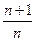 |
C.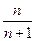 |
D.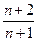 |
 的图象在点
的图象在点 与点
与点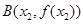 处的切线互相垂直,并交于点
处的切线互相垂直,并交于点 ,则点
,则点