题目内容
下列命题中,正确的命题的序号是 :(1)空集是任何集合的子集;(2)设A⊆B,若a∉B,则a∉A;(3)本班成绩优秀的学生可组成的集合;(4)设A=(x,y)|a1x+b1y+c1=0,B=(x,y)|a2x+b2y+c2=0,则方程(a1x+b1y+c1)(a2x+b2y+c2)=0的解集为A∪B.
分析:根据空集是不含任何元素的集合故其为任何集合的子集;A⊆B??x∈A则x∈B;集合的元素满足的三要素:确定性、互异性、无序性.
解答:解:对于(1),空集是任何集合的子集,是任何非空集合的真子集故(1)对
对于(2)∵A⊆B??x∈A则x∈B∴A⊆B,若a∉B,则a∉A对即(2)对
对于(3)“优秀”不确定,不满足集合的三要素故(3)不对
对于(4)∵(a1x+b1y+c1)(a2x+b2y+c2)=0?a1x+b1y+c1=0或a2x+b2y+c2=0,
故(a1x+b1y+c1)(a2x+b2y+c2)=0的解集为A∪B.故(4)对
故答案为(1)(2)(4)
对于(2)∵A⊆B??x∈A则x∈B∴A⊆B,若a∉B,则a∉A对即(2)对
对于(3)“优秀”不确定,不满足集合的三要素故(3)不对
对于(4)∵(a1x+b1y+c1)(a2x+b2y+c2)=0?a1x+b1y+c1=0或a2x+b2y+c2=0,
故(a1x+b1y+c1)(a2x+b2y+c2)=0的解集为A∪B.故(4)对
故答案为(1)(2)(4)
点评:本题考查空集的性质:空集是任何集合的子集,是任何非空集合的真子集,集合元素的性质:确定性、互异性、无序性.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足 对一切
对一切 恒成立,当
恒成立,当 时,
时, 。则下列四个命
。则下列四个命 是以4为周期的周期函数; ②
是以4为周期的周期函数; ② 上的解析式为
上的解析式为 ;
; ; ④
; ④ 处的切线方程为
处的切线方程为 。
。 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足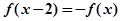 对一切
对一切 恒成立,当
恒成立,当 时,
时, 。则下列四个命
。则下列四个命 是以4为周期的周期函数; ②
是以4为周期的周期函数; ② 上的解析式为
上的解析式为 ;
; ; ④
; ④ 处的切线方程为
处的切线方程为 。
。