题目内容
已知数列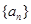 的前
的前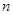 项和为
项和为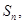 且
且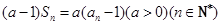 .
.
(1)求证数列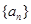 是等比数列,并求其通项公式
是等比数列,并求其通项公式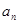 ;
;
(2)已知集合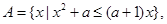 问是否存在实数
问是否存在实数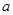 ,使得对于任意的
,使得对于任意的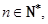 都有
都有 ? 若存在,求出
? 若存在,求出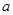 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】
(1)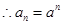 ;(2)
;(2) 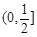 。
。
【解析】(1)当n=1时可先求出a1.
当n>1时,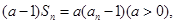
得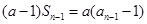
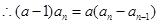 ,变形得
,变形得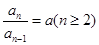
从而可得数列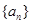 是等比数列,进而可求出其通项公式.
是等比数列,进而可求出其通项公式.
(2)要分a=1和a>1和0<a<1三种情况分别研究集合A,再研究是否满足题目条件.
(1)当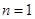 时,
时,
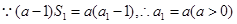
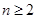 时,由
时,由
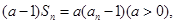 得
得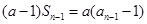
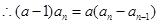 ,变形得
,变形得
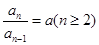 故
故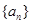 是以
是以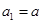 为首项,公比为
为首项,公比为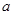 的等比数列,
的等比数列,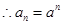 ---5分
---5分
(2)①当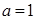 时,
时, 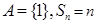 , 只有
, 只有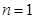 时,
时,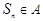 , 所以
, 所以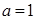 不合题意 ----7分
不合题意 ----7分
②当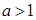 时,
时, 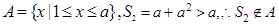 -----9分
-----9分
③当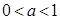 时,
时, 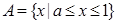 ,
,
而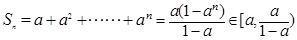 , 对任意
, 对任意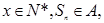

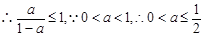 综上,a的取值范围是
综上,a的取值范围是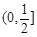 -------------12分
-------------12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
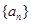 的前
的前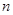 项和为
项和为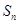 ,且
,且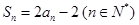 ,数列
,数列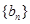 满足
满足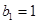 ,且
,且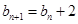 .
. 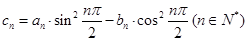 ,求数列
,求数列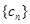 的前
的前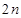 项和
项和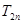 .
. 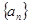 的前
的前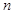 项和为
项和为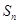 ,且
,且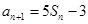
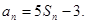 则
则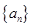 的前
的前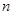 项和为
项和为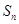 ,且对任意正整数
,且对任意正整数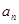 是
是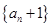 为等比数列;
为等比数列;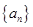 的前
的前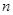 项和为
项和为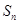 ,且
,且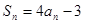 (
(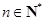 ).
).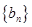 满足
满足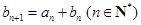 ,且
,且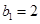 ,求数列
,求数列 的前
的前 项和为
项和为 ,且
,且 (
( ).
). 满足
满足 ,且
,且 ,求数列
,求数列