题目内容
(本题满分12分)
已知数列 的前
的前 项和为
项和为 ,且
,且 (
( ).
).
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)若数列 满足
满足 ,且
,且 ,求数列
,求数列 的通项公式.
的通项公式.
【答案】
(Ⅰ)证明:由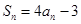 ,
,
 时,
时, ,解得
,解得 .----- -------------1分
.----- -------------1分
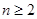 时,
时,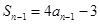
所以当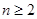 时,
时, ,--------------3分
,--------------3分
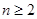 时,②-①得:
时,②-①得: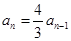 ---------------------------4分
---------------------------4分
又 ,-------------------------------------------5分
,-------------------------------------------5分
所以 是首项为1,公比为
是首项为1,公比为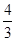 的等比数列-----------------6分
的等比数列-----------------6分
(Ⅱ) 因为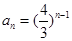 ,-----------------------------------------7分
,-----------------------------------------7分
由 ,得
,得 .
.
可得 -----------8分
-----------8分
=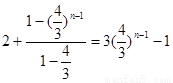 ,(
,(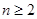 ),-----------10分
),-----------10分
当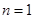 时也满足,----------------------------------------11分
时也满足,----------------------------------------11分
所以数列 的通项公式为
的通项公式为 .-----------------12分
.-----------------12分
【解析】

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面