题目内容
（2010•湖北模拟）若圆O1：x2+y2=36与圆O2：（x-m）2+y2=64（m∈R）相交于A、B两点，且两圆在点A处的切线互相垂直，则线段AB的长度是
．
| 48 |
| 5 |
| 48 |
| 5 |
分析：画出草图，O1A⊥AO2，有勾股定理可得m的值，再用等面积法，求线段AB的长度．
解答：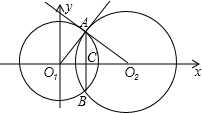
解：由题意得：圆O1（0，0），r1=6，O2（m，0），r2=8，
∴2＜|m|＜14，
∵O1A⊥AO2，
∴在Rt△AO1O2中，根据勾股定理得：O1O22=O1A2+O2A2，
即m2=62+82=36+64=100，
∴m=10或m=-10（不合题意，舍去），
则线段AB的长度为2AC=2×
=2×
=
．
故答案为：
解：由题意得：圆O1（0，0），r1=6，O2（m，0），r2=8，∴2＜|m|＜14，
∵O1A⊥AO2，
∴在Rt△AO1O2中，根据勾股定理得：O1O22=O1A2+O2A2，
即m2=62+82=36+64=100，
∴m=10或m=-10（不合题意，舍去），
则线段AB的长度为2AC=2×
| AO1•AO2 |
| O1O2 |
| 6×8 |
| 10 |
| 48 |
| 5 |
故答案为：
| 48 |
| 5 |
点评：此题考查了圆的标准方程，直线与圆的位置关系，利用了数形结合的思想，画出相应的图形是解本题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
（2010•湖北模拟）如图，正方体AC1的棱长为1，连接AC1，交平面A1BD于H，则以下命题中，错误的命题是（ ）
（2010•湖北模拟）如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．