题目内容
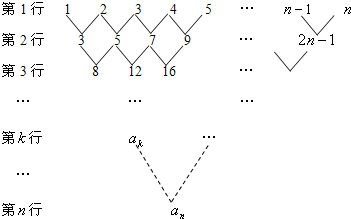
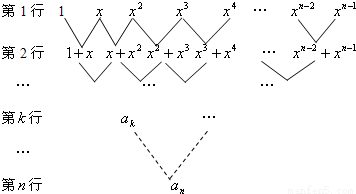
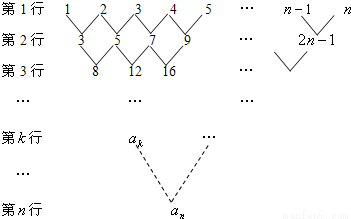
如图是一个三角形数阵.从第二行起每一个数都等于它肩上两个数的和,第k行的第一个数为ak(1≤k≤n,n≥2,k、n∈N*).(Ⅰ)写出ak与ak-1的递推关系,并求an;
(Ⅱ)求第k行所有数的和Tk;
(Ⅲ)求数阵中所有数的和Sn=T1+T2+…+Tn;并证明:当n≥2时,Sn≥2an.
【答案】分析:(Ⅰ) 通过前几项归纳可得:ak=2ak-1+2k-2(k≥2,且k∈N*),从而数列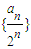 是以
是以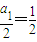 为首项,以
为首项,以 为公差的等差数列,可求出an;
为公差的等差数列,可求出an;
(Ⅱ) 由数阵的排布规律可知,每行的数(倒数两行另行考虑)都成等差数列,且公差依次为:1,2,22,…,2k-1,…第k行的首项为ak,项数为n+1-k,公差为2k-1
可求出Tn;
(Ⅲ)先求出Sn和an,然后利用作差法判定Sn-2an的符号,从而得到结论.
解答:解:(Ⅰ) 由题意得a1=1,a2=3=2a1+1,a3=8=2a2+2,a4=20=2a3+22,a5=48=2a4+23,
由以上归纳可得:ak=2ak-1+2k-2(k≥2,且k∈N*),(2分)
∴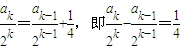 ,
,
∴数列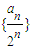 是以
是以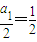 为首项,以
为首项,以 为公差的等差数列,
为公差的等差数列,
∴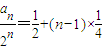 ,∴an=(n+1)•2n-2(n∈N*). (4分)
,∴an=(n+1)•2n-2(n∈N*). (4分)
(Ⅱ) 由数阵的排布规律可知,每行的数(倒数两行另行考虑)都成等差数列,
且公差依次为:1,2,22,…,2k-1,…
第k行的首项为ak,项数为n+1-k,公差为2k-1
∴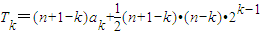
=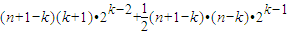
=(n+1-k)•2k-2[(k+1)+(n-k)]=(n+1-k)(n+1)•2k-2(7分)
当k=n时,Tn=an=(n+1)•2n-2符合上式;
当k=n-1时,由排布规律知,Tn-1=Tn=an=(n+1)•2n-2也符合上式;
∴Tk=(n+1-k)(n+1)•2k-2(1≤k≤n;k,n∈N*). (8分)
(Ⅲ)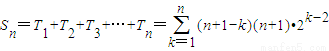 =
=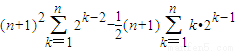
令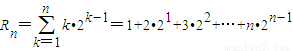 (1)
(1)
2Rn=1•2+2•22+3•23+…+(n-1)•2n-1+n•2n(2)
(1)-(2)得-Rn=1+2+22+…+2n-1-n•2n=2n-1-n•2n
∴Rn=(n-1)2n+1
∴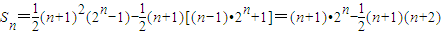 (n≥2,n∈N*)(12分)
(n≥2,n∈N*)(12分)
又an=(n+1)•2n-2
∴当n≥2时,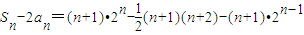 =
=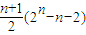
又2n=(1+1)n=Cn+Cn1+…+Cnn≥1+n+1=n+2(n≥2)
∴2n-n-2≥0(当且仅当n=2时取等号).
∴当n≥2时,Sn≥2an. (14分)
点评:本题主要考查了数列的通项公式,以及数列的递推关系和数列的求和方法同时考查了利用作差法判定大小关系,是一道综合题,有一定的难度.
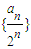 是以
是以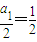 为首项,以
为首项,以 为公差的等差数列,可求出an;
为公差的等差数列,可求出an;(Ⅱ) 由数阵的排布规律可知,每行的数(倒数两行另行考虑)都成等差数列,且公差依次为:1,2,22,…,2k-1,…第k行的首项为ak,项数为n+1-k,公差为2k-1
可求出Tn;
(Ⅲ)先求出Sn和an,然后利用作差法判定Sn-2an的符号,从而得到结论.
解答:解:(Ⅰ) 由题意得a1=1,a2=3=2a1+1,a3=8=2a2+2,a4=20=2a3+22,a5=48=2a4+23,
由以上归纳可得:ak=2ak-1+2k-2(k≥2,且k∈N*),(2分)
∴
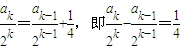 ,
,∴数列
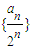 是以
是以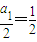 为首项,以
为首项,以 为公差的等差数列,
为公差的等差数列,∴
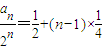 ,∴an=(n+1)•2n-2(n∈N*). (4分)
,∴an=(n+1)•2n-2(n∈N*). (4分)(Ⅱ) 由数阵的排布规律可知,每行的数(倒数两行另行考虑)都成等差数列,
且公差依次为:1,2,22,…,2k-1,…
第k行的首项为ak,项数为n+1-k,公差为2k-1
∴
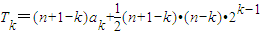
=
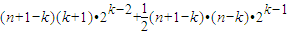
=(n+1-k)•2k-2[(k+1)+(n-k)]=(n+1-k)(n+1)•2k-2(7分)
当k=n时,Tn=an=(n+1)•2n-2符合上式;
当k=n-1时,由排布规律知,Tn-1=Tn=an=(n+1)•2n-2也符合上式;
∴Tk=(n+1-k)(n+1)•2k-2(1≤k≤n;k,n∈N*). (8分)
(Ⅲ)
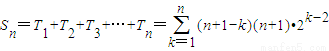 =
=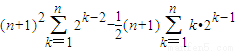
令
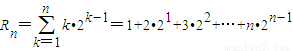 (1)
(1)2Rn=1•2+2•22+3•23+…+(n-1)•2n-1+n•2n(2)
(1)-(2)得-Rn=1+2+22+…+2n-1-n•2n=2n-1-n•2n
∴Rn=(n-1)2n+1
∴
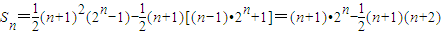 (n≥2,n∈N*)(12分)
(n≥2,n∈N*)(12分)又an=(n+1)•2n-2
∴当n≥2时,
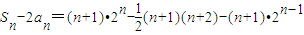 =
=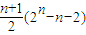
又2n=(1+1)n=Cn+Cn1+…+Cnn≥1+n+1=n+2(n≥2)
∴2n-n-2≥0(当且仅当n=2时取等号).
∴当n≥2时,Sn≥2an. (14分)
点评:本题主要考查了数列的通项公式,以及数列的递推关系和数列的求和方法同时考查了利用作差法判定大小关系,是一道综合题,有一定的难度.

练习册系列答案
相关题目