题目内容
已知以向量 为方向向量的直线l过点
为方向向量的直线l过点 ,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.
,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.(Ⅰ)求抛物线C的方程;
(Ⅱ)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若
 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.
【答案】分析:(Ⅰ)先求直线l: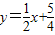 ,再根据抛物线的顶点关于直线l的对称点在该抛物线的准线上,可得方程,从而可求抛物线C的方程;
,再根据抛物线的顶点关于直线l的对称点在该抛物线的准线上,可得方程,从而可求抛物线C的方程;
(Ⅱ)设A(x1,y1),B(x2,y2),N(x,y),根据 ,用坐标表示,结合抛物线方程,即可求得点N的轨迹方程.
,用坐标表示,结合抛物线方程,即可求得点N的轨迹方程.
解答:解:(Ⅰ)由题意可得直线l: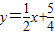 ①
①
过原点垂直于l的直线方程为 y=-2x ②
解①②得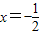 ,即两直线的交点的横坐标为
,即两直线的交点的横坐标为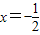 .
.
∵抛物线的顶点关于直线l的对称点在该抛物线的准线上.
∴ ,p=2
,p=2
∴抛物线C的方程为y2=4x.
(Ⅱ)设A(x1,y1),B(x2,y2),N(x,y),
由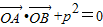 ,得x1x2+y1y2+4=0.
,得x1x2+y1y2+4=0.
又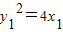 ,
,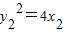 .
.
代入上式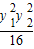 +y1y2+4=0.
+y1y2+4=0.
解得y1y2=-8
又直线ON: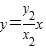 ,即
,即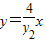
∵y=y1,∴y1y2=4x
∵y1y2=-8
∴x=-2(y≠0).
∴点N的轨迹方程为x=-2(y≠0).
点评:本题重点考查轨迹方程,考查抛物线的方程,考查向量知识,解题的关键是将向量关系转化为坐标之间的关系.
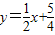 ,再根据抛物线的顶点关于直线l的对称点在该抛物线的准线上,可得方程,从而可求抛物线C的方程;
,再根据抛物线的顶点关于直线l的对称点在该抛物线的准线上,可得方程,从而可求抛物线C的方程;(Ⅱ)设A(x1,y1),B(x2,y2),N(x,y),根据
 ,用坐标表示,结合抛物线方程,即可求得点N的轨迹方程.
,用坐标表示,结合抛物线方程,即可求得点N的轨迹方程.解答:解:(Ⅰ)由题意可得直线l:
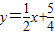 ①
①过原点垂直于l的直线方程为 y=-2x ②
解①②得
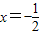 ,即两直线的交点的横坐标为
,即两直线的交点的横坐标为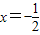 .
.∵抛物线的顶点关于直线l的对称点在该抛物线的准线上.
∴
 ,p=2
,p=2∴抛物线C的方程为y2=4x.
(Ⅱ)设A(x1,y1),B(x2,y2),N(x,y),
由
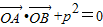 ,得x1x2+y1y2+4=0.
,得x1x2+y1y2+4=0.又
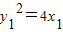 ,
,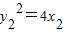 .
.代入上式
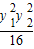 +y1y2+4=0.
+y1y2+4=0.解得y1y2=-8
又直线ON:
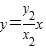 ,即
,即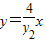
∵y=y1,∴y1y2=4x
∵y1y2=-8
∴x=-2(y≠0).
∴点N的轨迹方程为x=-2(y≠0).
点评:本题重点考查轨迹方程,考查抛物线的方程,考查向量知识,解题的关键是将向量关系转化为坐标之间的关系.

练习册系列答案
相关题目
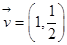 为方向向量的直线
为方向向量的直线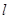 过点
过点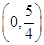 ,抛物线C:
,抛物线C: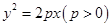 的顶点关于直线
的顶点关于直线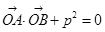 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程. 为方向向量的直线l过点
为方向向量的直线l过点 ,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.
,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上. (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.