题目内容
2.A、B是半径为R的球面上的两点,A、B是球面距离是$\frac{πR}{3}$,则过A、B两点的平面到球心的距离的最大值为$\frac{\sqrt{3}}{2}$R.分析 由球截面圆的性质,当截面是以AB为直径的圆时,球心到过A、B两点的平面的距离最大.设D为AB中点,OD即为所求.
解答 解:两点A、B间的球面距离为$\frac{πR}{3}$,∴∠AOB=$\frac{π}{3}$.
设过A、B两点的球截面为圆C,由球截面圆的性质OC为球心到过A、B两点的平面的距离.
D为AB中点,则OC≤OD,当且仅当C,D重合时取等号.
在边三角形AOB中,OD=$\frac{\sqrt{3}}{2}$R.
故答案为:$\frac{\sqrt{3}}{2}$R.
点评 本题考查球面距离的概念,点面距的计算.分析出何时区最大值是关键,考查了空间想象能力、推理论证、计算能力.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
12.如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是( )
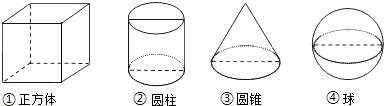

| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
17.函数y=ax+3-2(a>0,a≠1)的图象恒过定点A,若点A在直线$\frac{x}{m}+\frac{y}{n}$=-1上,m>0,n>0,则3m+n的最小值为( )
| A. | 13 | B. | 16 | C. | 11+6$\sqrt{2}$ | D. | 28 |
12.已知{an}是递增数列,对于任意的正整数n均有an=n2+λn恒成立,则实数λ的取值范围是( )
| A. | [-2,+∞) | B. | (-3,+∞) | C. | R | D. | ∅ |
 已知椭圆C的中心在原点,一个焦点和抛物线y2=8x的焦点重合,离心率等于$\frac{1}{2}$.
已知椭圆C的中心在原点,一个焦点和抛物线y2=8x的焦点重合,离心率等于$\frac{1}{2}$.