题目内容
11.已知函数f(x)在区间[1,3]上连续不断,且f(1)•f(2)•f(3)<0,则下列说法正确的是( )| A. | 函数f(x)在区间[1,2]或者[2,3]上有一个零点 | |
| B. | 函数f(x)在区间[1,2]、[2,3]上各有一个零点 | |
| C. | 函数f(x)在区间[1,3]上最多有两个零点 | |
| D. | 函数f(x)在区间[1,3]上有可能有无数个零点 |
分析 根据函数零点的判断得出①如果函数f(x)是单调函数,且f(1)<0,f(2)<0,f(3)<0,f(x)就无零点,排除A,B根据图形 判断C不正确,可得答案.
解答 解:函数f(x)在区间[1,3]上连续不断,且f(1)f(2)f(3)<0,
①如果函数f(x)是单调函数,且f(1)<0,f(2)<0,f(3)<0,
f(x)就无零点,
故:A,B不正确.
②如果函数f(x)不是单调函数,且f(1)<0,f(2)<0,f(3)<0,f($\frac{3}{2}$)>0,f($\frac{5}{2}$)>0,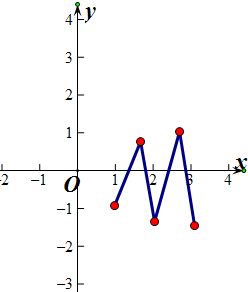
根据函数的零点判断方法得出:函数f(x)在区间[1,3]上有可能4个零点,
故:C不正确.
所以排除:A,B,C
故选:D.
点评 本题考查了函数零点的判断方法,考虑全面,结合图形判断求解,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
16.已知f(x)=2|x|+x2+a有唯一的零点,则实数a的值为( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
1.把函数y=sin3x的图象适当变化就可以得y=$\frac{{\sqrt{2}}}{2}$(sin3x-cos3x)的图象,这个变化可以是( )
| A. | 沿x轴方向向右平移$\frac{π}{4}$ | B. | 沿x轴方向向右平移$\frac{π}{12}$ | ||
| C. | 沿x轴方向向左平移$\frac{π}{4}$ | D. | 沿x轴方向向左平移$\frac{π}{12}$ |
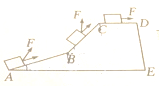 如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.
如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.