题目内容
已知f(x)=mx2+3(m-4)x-9(m∈R).(1)试判断函数f(x)的零点的个数;
(2)若函数f(x)有两个零点x1,x2,求d=|x1-x2|的最小值;
(3)若m=1,且不等式f(x)-a>0对x∈[0,2]恒成立,求实数a的取值范围.
【答案】分析:(1)分别讨论m=0和m≠0两种情况,利用一次函数和二次函数的零点判断方法分别判断零点个数;(2)利用韦达定理,将d=|x1-x2|转化为关于m的函数,利用配方法求最值即可;(3)将所求恒成立问题转化为求函数f(x)的最值问题,利用二次函数的单调性求函数f(x)在[0,2]上的最小值即可
解答:解:(1)当m=0时,f(x)=-12x-9,函数的零点为x=- ,即函数只有一个零点
,即函数只有一个零点
当m≠0时,△=9(m-4)2+36m=(m-2)2+12>0
∴函数f(x)的零点的个数为2
故当m=0时,函数f(x)的零点的个数为1;当m≠0时,函数f(x)的零点的个数为2
(2)若函数f(x)有两个零点x1,x2,则m≠0,
x1+x2=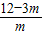 ,x1•x2=
,x1•x2=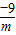
∴d=|x1-x2|=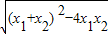 =
=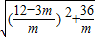 =12
=12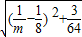 ≥12×
≥12×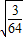 =
=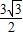 (m=8时取等号)
(m=8时取等号)
∴d=|x1-x2|的最小值为 ;
;
(3)若m=1,则f(x)=x2-9x-9
∴不等式f(x)-a>0对x∈[0,2]恒成立,即x2-9x-9>a对x∈[0,2]恒成立
只需f(x)在[0,2]上的最小值大于a
∵f(x)=x2-9x-9=(x- )2-
)2-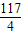 ≥f(2)=-23
≥f(2)=-23
∴a<-23
点评:本题考查了一次函数与二次函数零点判断方法,二次方程韦达定理的应用,不等式恒成立问题的解法及配方法求二次函数的最值
解答:解:(1)当m=0时,f(x)=-12x-9,函数的零点为x=-
 ,即函数只有一个零点
,即函数只有一个零点当m≠0时,△=9(m-4)2+36m=(m-2)2+12>0
∴函数f(x)的零点的个数为2
故当m=0时,函数f(x)的零点的个数为1;当m≠0时,函数f(x)的零点的个数为2
(2)若函数f(x)有两个零点x1,x2,则m≠0,
x1+x2=
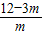 ,x1•x2=
,x1•x2=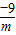
∴d=|x1-x2|=
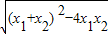 =
=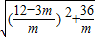 =12
=12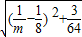 ≥12×
≥12×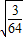 =
=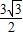 (m=8时取等号)
(m=8时取等号)∴d=|x1-x2|的最小值为
 ;
;(3)若m=1,则f(x)=x2-9x-9
∴不等式f(x)-a>0对x∈[0,2]恒成立,即x2-9x-9>a对x∈[0,2]恒成立
只需f(x)在[0,2]上的最小值大于a
∵f(x)=x2-9x-9=(x-
 )2-
)2-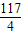 ≥f(2)=-23
≥f(2)=-23∴a<-23
点评:本题考查了一次函数与二次函数零点判断方法,二次方程韦达定理的应用,不等式恒成立问题的解法及配方法求二次函数的最值

练习册系列答案
相关题目
已知f(x)=x3+mx2+x+5,存在实数xo使f′(xo)=0,又f(x)是R上的增函数,则m的取值范围是( )
A、(-∞,-
| ||||
B、{-
| ||||
C、(-∞,-
| ||||
D、[-
|