题目内容
 已知抛物线y2=4ax(a>0且a为常数),F为其焦点.
已知抛物线y2=4ax(a>0且a为常数),F为其焦点.(1)写出焦点F的坐标;
(2)过点F的直线与抛物线相交于P、Q两点,且
| PF |
| FQ |
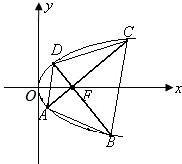
(3)若线段AC、BD是过抛物线焦点F的两条动弦,且满足AC⊥BD,如图所示.求四边形ABCD面积的最小值S(a).
分析:(1)根据抛物线的性质可知p=2a,进而焦点坐标为F(a,0).
(2)假设点为P(x0,y0)、Q(x1,y1),然后表示出
、
,再根据
=2
可以得到(a-x0,-y0)=2(x1-a,y1),再由y12=4ax1,y02=4ax0,可确定
=4a•
,进而可得x0=2a,y02=4ax0=8a2,即y0=±2
a,然后表示出直线PQ的斜率代入即可得到答案.
(3)设直线AC的斜率为kAC=k(k≠0),可得到AC的方程然后与抛物线联立得到两根之和、两根之积,根据弦长公式表示出|AC|并化简,然后根据直线AC的斜率可得到直线BD的斜率求出|BD|的弦长,再表示出S四边形ABCD运用基本不等式可确定答案.
(2)假设点为P(x0,y0)、Q(x1,y1),然后表示出
| PF |
| FQ |
| PF |
| FQ |
| ||
| 4 |
| 3a-x0 |
| 2 |
| 2 |
(3)设直线AC的斜率为kAC=k(k≠0),可得到AC的方程然后与抛物线联立得到两根之和、两根之积,根据弦长公式表示出|AC|并化简,然后根据直线AC的斜率可得到直线BD的斜率求出|BD|的弦长,再表示出S四边形ABCD运用基本不等式可确定答案.
解答:解:(1)∵抛物线方程为y2=4ax(a>0),∴焦点为F(a,0).
(2)设满足题意的点为P(x0,y0)、Q(x1,y1).
∵
=2
,
∴(a-x0,-y0)=2(x1-a,y1),即
.
又y12=4ax1,y02=4ax0,
∴
=4a•
,进而可得x0=2a,
=4ax0=8a2,即y0=±2
a.
∴kPQ=kPF=
=±2
.
(3)由题可知,直线AC既不平行x轴,也不平行y轴(否则AC,BD与抛物线不会有四个交点),
于是,设直线AC的斜率为kAC=k(k≠0),则AC的方程为:y=k(x-a).
联立方程组
,化简得k2x2-2a(k2+2)x+k2a2=0(设点A(x1,y1)、C(x2,y2)),
则x1、x2是此方程的两个根.
∴
.
∴弦长|AC|=|x1-x2|
=
=
=4a
.
又AC⊥BD,∴kBD=-
.
于是,弦长|BD|=4a
=4a(1+k2).
∴S四边形ABCD=
|AC|•|BD|=8a2
=8a2(k2+
+2)≥32a2(当且仅当k2=
,即k=±1时,等号成立).
∴S(a)=32a2.
(2)设满足题意的点为P(x0,y0)、Q(x1,y1).
∵
| PF |
| FQ |
∴(a-x0,-y0)=2(x1-a,y1),即
|
又y12=4ax1,y02=4ax0,
∴
| ||
| 4 |
| 3a-x0 |
| 2 |
| y | 2 0 |
| 2 |
∴kPQ=kPF=
| y0-0 |
| x0-a |
| 2 |
(3)由题可知,直线AC既不平行x轴,也不平行y轴(否则AC,BD与抛物线不会有四个交点),
于是,设直线AC的斜率为kAC=k(k≠0),则AC的方程为:y=k(x-a).
联立方程组
|
则x1、x2是此方程的两个根.
∴
|
∴弦长|AC|=|x1-x2|
| 1+k2 |
=
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
| 1+k2 |
(
|
=4a
| 1+k2 |
| k2 |
又AC⊥BD,∴kBD=-
| 1 |
| k |
于是,弦长|BD|=4a
1+(-
| ||
(-
|
∴S四边形ABCD=
| 1 |
| 2 |
| (1+k2)2 |
| k2 |
=8a2(k2+
| 1 |
| k2 |
| 1 |
| k2 |
∴S(a)=32a2.
点评:本题主要考查抛物线和直线的综合问题.直线和圆锥曲线的综合题一般作为高考的压轴题出现,要想解答正确,就必须对基础知识熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

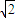 ,过抛物线C1的焦点F作倾斜角为
,过抛物线C1的焦点F作倾斜角为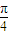 的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线C1于一点Q(点Q在x轴下方).
的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线C1于一点Q(点Q在x轴下方).