题目内容
已知抛物线y2=4a(x+a)(a>0),过原点O作一直线交抛物线于A、B两点,如图所示,试求|OA|·|OB|的最小值。

解:设直线AB的参数方程为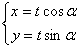 (t为参数)
(t为参数)
代入y2=4a(x+a)中得:t2sin2α-4atcosα-4a2=0
∴|OA||OB|=|t1t2|=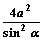 ≥
≥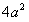
当 时,|OA||OB|取最小值
时,|OA||OB|取最小值 。
。
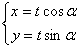 (t为参数)
(t为参数)代入y2=4a(x+a)中得:t2sin2α-4atcosα-4a2=0
∴|OA||OB|=|t1t2|=
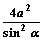 ≥
≥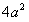
当
 时,|OA||OB|取最小值
时,|OA||OB|取最小值 。
。
练习册系列答案
相关题目
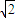 ,过抛物线C1的焦点F作倾斜角为
,过抛物线C1的焦点F作倾斜角为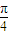 的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线C1于一点Q(点Q在x轴下方).
的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线C1于一点Q(点Q在x轴下方).