题目内容
三棱柱 中,
中,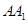 与
与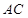 、
、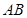 所成角均为
所成角均为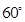 ,
, ,且
,且 ,则三棱锥
,则三棱锥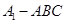 的体积为( )
的体积为( )
 中,
中,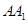 与
与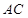 、
、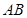 所成角均为
所成角均为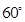 ,
, ,且
,且 ,则三棱锥
,则三棱锥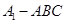 的体积为( )
的体积为( )A.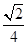 | B.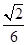 | C.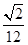 | D.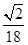 |
C
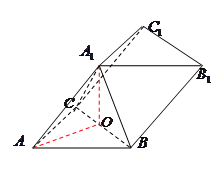
试题分析:连接
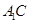 ,由已知得
,由已知得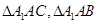 为正三角形,
为正三角形,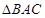 为等腰直角三角形,所以有
为等腰直角三角形,所以有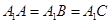 所以
所以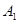 在底面
在底面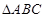 上的射影是等腰直角
上的射影是等腰直角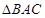 的外心,即为
的外心,即为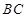 中点,取
中点,取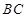 中点
中点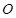 ,连接
,连接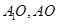 在直角
在直角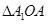 中,
中,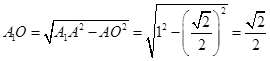 ,又
,又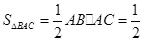 ,所以
,所以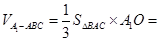
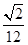 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


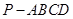 中,底面
中,底面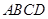 是矩形,
是矩形,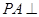 平面
平面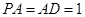 ,
,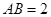 ,
,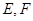 分别是
分别是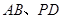 的中点.
的中点.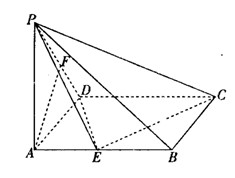
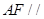 平面
平面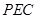 ;
; 的余弦值.
的余弦值.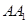 、
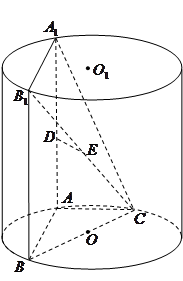
、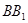 为圆柱
为圆柱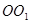 的母线,
的母线,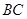 是底面圆
是底面圆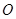 的直径,
的直径,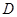 、
、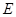 分别是
分别是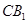 的中点,
的中点,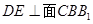 .
.
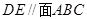 ;
;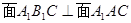 ;
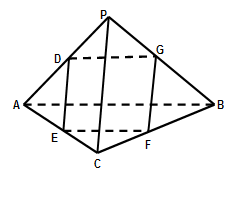
;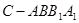 与圆柱
与圆柱 所在的平面与正方形
所在的平面与正方形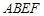 所在的平面相互垂直,
所在的平面相互垂直,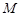 、
、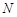 分别是
分别是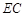 、
、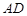 的中点.
的中点.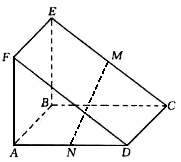
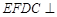 面
面 ;
;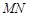 与平面
与平面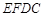 所成的角正弦值.
所成的角正弦值.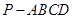 的底面是正方形,
的底面是正方形,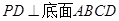 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=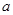 ,
,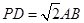
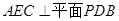 ;
; 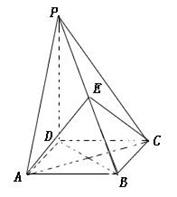
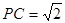 ,求四面体PABC的体积.
,求四面体PABC的体积.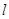 、
、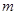 与平面
与平面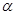 、
、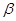 的命题中,正确的是 ( )
的命题中,正确的是 ( )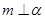 ,
,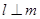 ,则
,则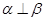 ,
,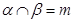 ,
,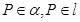 ,且
,且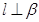
 ,
,